| Day |
Date |
Activity |
Assignment (reading assignments are due the day they appear on the calendar) |
| Mon | 1/14 |
Welcome |
Read the preface and chapter #1 for Wednesday |
| Wed | 1/16 |
Primitive Counting |
- Explain how the children's game of "musical chairs" works, using the notion of one-to-one correspondence. How else is the idea of one-to-one correspondence used in life? We can sometimes use it to avoid counting!
- Do a little web research on the Ishango bone. Where did it come
from? How long ago was it made? What was it made from?
- Use the method of "primitive counting" described in class to write
the representation of
- 89
- 96
- What numbers are represented as
- 1,0,0,1,0,1,1
- 1,1,1,0,0,1
- What special sorts of numbers are represented as
- 1
- 1,0
- 1,0,0
- 1,0,0,0
- 1,0,0,0,0
etc.?
|
| Fri | 1/18 |
|
Learn to perform the "counting card trick" that was described in class. Try to figure out why it works....
|
| Mon | 1/21 |
MLK Day |
|
| Wed | 1/23 |
Prime and Composite Numbers |
Chapters 2 (and also 25, but 2 is more important). Homework:
- Using pennies, rocks, turnips, or whatever, discover the
first composite number that can be expressed as
three distinctly different rectangles (not
counting the "line of pennies" rectangle).
- The number 12 can be expressed as two distinctly
different rectangles (rotations of a rectangle don't
count as "distinctly different"). What is the first
triangular number that can be expressed as exactly two
distinctly different rectangles?
- What are the next three numbers, after 12, that can be expressed
as exactly two distinctly different rectangles?
- We talked about squares, triangles, rectangles: how should we
think about those numbers called "cubes" in terms of pennies?
What are some of the first cubes, and what would they look like
represented using pennies?
- What are the hexagonal numbers? (A regular hexagon has six equal
sides, and six equal angles.) Can you see a hexagon in the
image below? Pick out a single penny near the middle, and look
at its neighbors:

|
| Fri | 1/25 |
|
- Use trees to write the prime factorizations of the following:
- 15015
- 1763
- You could play the "3 card trick" with only 6 or 7 cards, instead
of 52 cards -- but it's not so impressive, is it? Work the card trick
backwards, starting from 3 cards. Do you see that you could have
started with either 6 or 7 cards? In either case, the three cards would
have been numbered 2,4,6. Continuing to work backwards, what would come
in the next step, depending on whether you began 6 or 7 cards?
|
| Mon | 1/28 |
Babylonian/Mayan Math |
Chapter 6 |
| Wed | 1/30 |
|
Read this on-line intro to Mayan Math
- Write the following numbers (written in our system) in the
Babylonian and Mayan systems:
- 1763
- 15015
- 3661
- How would you tap out your name in Morse code?
|
| Fri | 2/1 |
|
|
| Mon | 2/4 |
Bases |
- Write the following numbers in each of the bases 2, 8, and 16:
- 42
- 63
- 1024
- 1984
- 2013
- Try to figure out how Lewis Carroll was using unusual
bases to do the strange math in chapter two of Alice
in Wonderland? On about the third page of chapter
two (after the graphic of "Giant Alice watching Rabbit
run away"), Alice starts speaking out some bizarre
equations:
"Let me see: four times five is twelve, and four times
six is thirteen, and four times seven is -- oh dear! I
shall never get to twenty at that rate!"
Find some reasonable bases (you'll need several!) to make the
"calculations" work out....
|
| Wed | 2/6 |
binary (base 2) |
- Use primitive counting to write the string for the following numbers of sheep:
- 37
- 97
- 163
- Write each number in binary:
- 37
- 97
- 163
- How do you write each of these Mersenne Primes in binary?
- 3=2^2-1
- 7=2^3-1
- 31=2^5-1
- 127=2^7-1
- 2^{57,885,161}-1 (don't try this one on a piece of paper!:)
- How many sheep? Here are the primitive counting strings, you priest you:
- 11011
- 101011
- 100100001
Check out these other base videos:
- Schoolhouse Rock strikes again:
Little Twelve Toes (guess the base!)
- Tom Lehrer strikes, too: New
Math -- a lesson in base-8 arithmetic
|
| Fri | 2/8 |
Egyptian Multiplication |
- Please visit the webpage at this link and read it over for next time.
- Demonstrate Egyptian multiplication by multiplying:
|
| Mon | 2/11 |
Egyptian Math |
- Try another Egyptian multiplication, and make sure that you're ready for the upcoming test:
- Demonstrate Egyptian division by dividing:
- Read Chapter 5, p. 29.
|
| Wed | 2/13 |
|
Demonstrate Egyptian division by dividing the following using both methods, if
you can! That is, using the multiplication table backwards, and using the unit
fraction table. One method may be easier than the other!
|
| Fri | 2/15 |
Review |
|
| Mon | 2/18 |
Exam I |
|
| Wed | 2/20 |
Greek Math |
Chapters 4 and 12 |
| Fri | 2/22 |
Pythagorean Theorem |
Finish off the worksheet that was distributed in class:
- If the longest side is longer than the Pythagorean theorem would suggest, then the triangle is obtuse;
- If the longest side is shorter than the Pythagorean theorem would suggest, then the triangle is acute.
- Also see if you can follow our proof of the Pythagorean theorem, as presented on the last page.
|
| Mon | 2/25 |
Irrational numbers |
- If a right triangle has legs of length 1 and x, what is the length of the hypotenuse?
- On a sunny and windy day, a student flies a kite on the level college green just to relax. Her kite takes off and soars. She lets all 150 feet of the string out and attracts a crowd of onlookers. A spectator 90 feet away from the student notices that the kite is directly above him. Unlike a real kite this math-question kite has the string going in a perfectly straight line from the student to the kite. How high is the kite above the ground?
- A sailboat has a tall mast. The backstay (the heavy steel cable that attaches the top of the mast to the back, or stern, of the sailboat) is made of 130 feet of cable. The base of the mast is 50 feet from the stern of the boat. How tall is the mast?
(Problems from The Heart of Mathematics)
Read the pages (also from The Heart of Mathematics) at this link:
http://www.nku.edu/~longa/classes/mat115_resources/docs/Heart/IrrationalHeart/. Then show that the
 is irrational. is irrational.
|
| Wed | 2/27 |
Indians, Chinese, and Pascal |
- Write the next line in the Chinese version of Pascal's Triangle.
- Write the next line in the Jewish/Arabic/Hindu version of Pascal's Triangle.
- Pascal's triangle contains numbers like the triangular and the
tetrahedral numbers. What would be call the numbers after the
tetrahedral numbers? Explore these numbers: 1, 5, 15, 35, 70,
126, ....
|
| Fri | 3/1 |
Fibonacci and his Nim |
Play Nim with someone, and see if you can always win:
- Try it with 18 counters. Is it better to go first or second?
- Try it with 21 counters. Is it better to go first or second?
- Try it with 28 counters. Is it better to go first or second?
- Try it with 34 counters. Is it better to go first or second?
Read the biography of Leonardo
Pisano Fibonacci. You'll see references to some of the mathematics we've
already done in this course!
|
| Mon | 3/4 |
Fibonacci Nim |
Same assignment as before, only now you know the strategy. See if you can always win!
|
| Wed | 3/6 |
Graphs |
Chapters 3, 24, and 26
Homework (This one is due: Monday, 3/18 -- a good job on this will replace a
quiz): I want you to visit this
website and turn your own image into a Fibonacci spiral. Choose an
appropriate image, then create and then email me a copy of your own spiral
image. Make one that everyone will enjoy, as I will create a gallery of
images. There may also be prizes for the winners.
Make sure that you send me the final image, and not just a link
(that won't do anything!). Right click on the image, and save it to
your computer -- then paste the image into your email. That's the
easiest way, I think.
One more thing: the image won't last on the server for very long, so download it right away.
|
| Fri | 3/8 |
|
|
| Mon | 3/11 |
Spring Break |
|
| Wed | 3/13 |
Spring Break |
|
| Fri | 3/15 |
Spring Break |
|
| Mon | 3/18 |
|
Please read this short piece on graphs; the other readings for this unit have examples of graphs, which I will point out after our general discussion of the history of graphs.
|
| Wed | 3/20 |
More Graphs: Example from our readings |
Homework:
- Draw the complete graph with 8 vertices. How many edges are there?
- Draw all the distinctly different simple graphs with five vertices. There are a lot! How many? Use symmetry as much as you can to avoid double counting them. Can you see any patterns in how they're created?
|
| Fri | 3/22 |
Exam II |
|
| Mon | 3/25 |
More Graphs |
- Check out this page and relate it to Euler's Konigsberg problem. Try some of the puzzles yourself.
- Write down the update equations (see p. 195 of our text) for this "toy web":
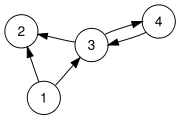 You might rename the vertices 1=x, 2=y, 3=z, 4=w, for example,
to make writing the equations easier (so that they look more
like the equations in the text).
You might rename the vertices 1=x, 2=y, 3=z, 4=w, for example,
to make writing the equations easier (so that they look more
like the equations in the text).
|
| Wed | 3/27 |
Algebra |
Chapters 7 and 10; here's a bit of homework:
- Tchapo was five times older than Thad at one time, then, four
years later, Tchapo was only three times older. How many years older is
Tchapo than Thad?
- If you add the age of a man to the age of his wife, the result is 91. He is now twice as old as she was when he was as old as she is now. How old is the man and his wife?
- Is the answer from the previous problem an example of an "icky relationship", according to chapter 7?
|
| Fri | 3/29 |
More Algebra |
|
| Mon | 4/1 |
|
- What's your non-icky relationship range?
- At what age do the two ages x and y equal each
other?
- What range do you get for a 12-year old? In what sense does that
make sense?
|
| Wed | 4/3 |
Geometry and Topology |
Chapter 27
- Twist a band in two different ways:
- four times, and
- five times,
and cut the band in "two". What objects result? Describe them exactly,
specifying their number of half twists, how they're connected, etc.
- Describe exactly what you get if you cut a thrice-twisted band in thirds
(as we did in class to the Mobius band, which is only
once-twisted). You need a pretty long band to do this!
- Make sure that you can make the two distinctly different Mobius
bands (they're mirror images of each other). Symmetry is a very
important mathematical idea.
- Relate the following logo to twisted bands (e.g. Mobius bands):

- Is the following recycling symbol correct (i.e. Mobius) or not?
 How can you tell? The true recycling symbol is not symmetric under
rotation: rotate it, and it looks different.
How can you tell? The true recycling symbol is not symmetric under
rotation: rotate it, and it looks different.
- Find two examples of the recycling symbol on nationally known products,
one Mobius and the other not Mobius. Which products know what
they're doing?
- Think about what kind of math would look good (and play well) on
the Mobius Music Box. I'll take suggestions, and then either
compose some myself, or let you try....
|
| Fri | 4/5 |
Probability |
Chapter 23; Please read this
chapter from Tony Crilly's "50 Mathematical Ideas You Really Need to
Know". It gives the basics of probability.
|
| Mon | 4/8 |
I've added another probability reading on the assignment page: this
chapter about the birthday problem from Tony Crilly's "50
Mathematical Ideas You Really Need to Know".)
Hopefully this will help you understand this remarkable result!
|
- What is the probability that 5 randomly chosen people
will have a common birthday?
- What is the probability of getting exactly one even die on a roll
in a fair game of craps?
- What is the probability of tossing three heads in a row on three
tosses of a fair coin?
- What is the probability that two throws of an ordinary fair die
will give two different results? that three tosses will give three
different results? that six tosses will give six different results?
that seven tosses will give seven different results?
|
| Wed | 4/10 |
Conditional Probability |
Do the "plant problem" from chapter 23 again, but change the numbers: assume that
-
=.75})
-
=.14})
-
=.40})
That is, the plant's not ailing as badly, it seems (probabilities of death have gone down); but your friend is more unreliable than ever! Find the probability that your plant dies.
|
| Fri | 4/12 |
More Conditional Probability |
Now retry the breast cancer problem: suppose that
-
=.012})
-
=.95})
-
=.03})
Now solve for these probabilities:
|
| Mon | 4/15 |
Statistics |
Chapter 22 |
| Wed | 4/17 |
|
|
| Fri | 4/19 |
Exam III |
|
| Mon | 4/22 |
Fractals and Infinity |
Chapters 8, 16, and 30 |
| Wed | 4/24 |
Fractals
Please read this
chapter from Tony Crilly's "50 Mathematical Ideas You Really Need to
Know". It gives the basics of fractals.
|
Homework: give the following a try, to prepare for the statistics quiz on Friday: Distribution practice
Also try my funhouse mirror generator: make your own funhouse mirror
image, using my web
interface and your own image, and I'll post them to our website.
|
| Fri | 4/26 |
Fractals |
Try these homework problems.
Create your own examples of
- a stick fractal, and
- an area fractal.
You'll need to
- Define the simple rule (e.g. how does a stick turn into other sticks?)
- Apply the rule at least twice, so that we can begin to see "the world within the world"
|
| Mon | 4/29 |
Infinity |
|
| Wed | 5/1 |
More infinity (can that be?) |
Homework:
- What is the power set of the four Beatles,
 ? ?
- What does the 6th line of Pascal's triangle tell us about the kinds of sets in the power set of a set with five elements?
- Which is bigger: all integers (including the negative ones) or the even natural numbers?
- Which is bigger: all prime numbers, or all Fibonacci numbers?
|
| Fri | 5/3 |
Logo Day |
|


