Day 8, MAT115

Last Time

Next Time

Announcements:
- Quiz today (last 15 minutes). It will involve primes and prime factorization, and Babylonian math.
Here's our "Question of the day":

Might trees be useful to organize ourselves when writing numbers in different systems?
First let's review what we discovered about the Mayans:
- There are three distinct symbols in their system: the zero symbol (loaf of bread), the dit, and the dah (dot and line segment, 1 and 5 respectively).
- Their system is also positional (although they stacked numbers vertically).
- Their base is 20: they used powers of twenty for their stacks.
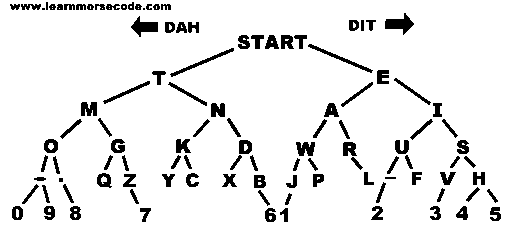
Last time we also looked into the system of Morse code, and saw that it is based on two symbols, and that a tree structure was used to summarize the coding of each letter and number. Furthermore, there was a nice structure for the encoding of each digit 0 to 9.

This tree is useful for both learning the coding for each symbol (including digits -- do you know all 10 digits now?), and also for the actual encoding and decoding process.
How might we use trees to do our writing of any particular type of number system, e.g. Mayan or Babylonian (or our own)? Let's take a look at a few numbers, and see how to operate.
In the case of the Babylonians we use powers of 60: 1=60⁰, 60=60¹, 3600=60², 216000=60³,....
In the case of the Mayans we use powers of 20: 1=20⁰, 20=20¹, 400=20², 8000=20³,....
In both cases the process is the same:
1. divide the number by the largest power possible,
2. remove the most multiples of the largest power possible, then
3. "do it again" with the remainder.
And we'll store the results in a tree. Let's try a few:
1. 5432
2. 22319
3. 498
Suppose that there was some crazy society that used 16 as its base. Maybe these folks use only fingers and toes, but not the thumbs or big toes! How would we write each of these numbers using that base?
Assume that this "crazy society" uses our ten digits, then uses A, B, C, D, E, and F as the symbols for the next six "digits".
In this case we use powers of 16: 1=16⁰, 16=16¹, 256=16², 4096=16³,....
Quiz

Links:

Website maintained by Andy Long. Comments appreciated.