Day 19, MAT115

The Indians knew of the primitive Pythagorean triples

as early as the 8th century BCE. (Source)

• This triangle is much older than Blaise Pascal, who lived in the 17th century (it dates also to China, long before -- 13th century AD). But the Indians were considering it as early as the 4th center BCE (Pingala).

  Here's how a 10th century AD manuscript described Pingala's approach to the constructing the triangle:

  "Draw a square. Beginning at half the square, draw two other similar squares below it; below these two, three other squares, and so on. The marking should be started by putting 1 in the first square. Put 1 in each of the two squares of the second line. In the third line put 1 in the two squares at the ends and, in the middle square, the sum of the digits in the two squares lying above it. In the fourth line put 1 in the two squares at the ends. In the middle ones put the sum of the digits in the two squares above each. Proceed in this way. Of these lines, the second gives the combinations with one syllable, the third the combinations with two syllables, ..."

  So what would be the next line in the table above?

• While we don't have the BCE Indian version of the table, we do have a version from a Jewish mathematician who converted to Islam (and used Arabic numerals -- thanks Mark Middendorf for the graphic):

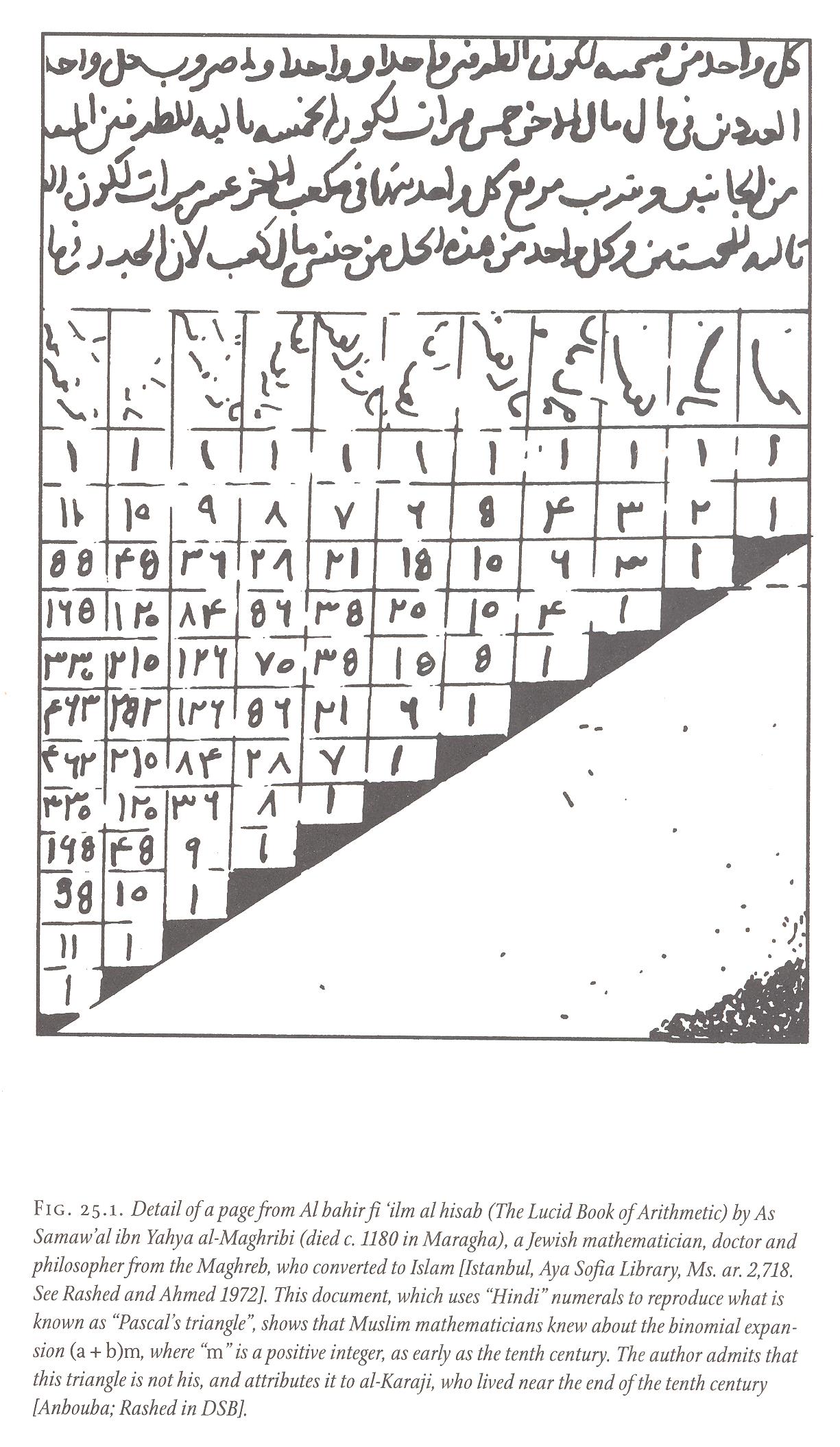
  (from the marvellous book The Universal History of Numbers, by Georges Ifrah).

• Here is a magnificent Chinese version:

  This allows us to do is to understand how this culture wrote its numbers (Chinese Bamboo Counting Rods). How did the Chinese of the 13th century write 15? 28? 30?

• A tiling of hexagons makes a particularly nice display:
  

  except that, like the Chinese version, there's a mistake in one row. I found by exploring a conjecture that Stephanie Guffey proposed: that the elements in some rows are multiples of the representive number of that row. For example, the "7" row, all but the ones at the ends are multiples of 7. I noted that it isn't true for every row, but wondered if it might be true for prime numbers. When I checked to see, that's when I found the error!

  Stephanie will always be famous for helping me find this error....

  Here's an updated hexagonal version of Pascal's triangle:

  

• What's it good for?
  • Pascal was interested in gambling -- that's why he studied it so hard. He was interested in what we call combinatorics, which includes the study of the number of ways of doing particular things. For example,
    How many ways can you put 7 people into 2 cars to go to the party?

  • What do you notice about the sum of the numbers in each row? Here's how mathematicians write it:

    

  • Various kinds of numbers appear in the triangle:
    • Bunches of ones down the side, followed by a line of natural numbers, 1, 2, 3, 4, ....

    • The Triangular numbers appear in Pascal's triangle.
    • So do the Tetrahedral numbers

    • What's next? What would we call the numbers after those? How can we represent those geometrically?