Day 28, MAT115

Last Time

Next Time

Announcements:
- Your exams are due, corrected, by this Friday at class time.
- The spiral gallery votes are also due by Friday. Thanks to you who have already voted.
Today's Question of the Day:

Suppose the length of a hallway is y when measured in yards, and f when measured in feet. What is an equation that relates y to f?
Let's start, however, by taking a peek at the homework problems.
The quiz Friday will cover graphs. Do you know the definition of a graph? Have you tried out your homework?
- If you drew the complete graph with 8 vertices, how many edges are there?
- I asked you to graph all the simple graphs on five vertices. How many are there?
  These represent all the possible connections between five people, for example.
  My graphic of all the simple graphs on five vertices is designed to show you a certain symmetry (or duality) between the graphs.
  1. How many are connected (so that everyone can get a message to everyone else)?
  2. How many contain an isolated person (of degree 0)?
  3. How many are fully redundant (so that if a single connection is broken, everyone can still pass messages around)?
- Here are the questions for the second homework on graphs:
  1. Check out this page and relate it to Euler's Konigsberg problem. Try some of the puzzles yourself.
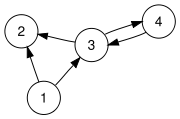
  2. Write down the update equations (see p. 195 of our text) for this "toy web": You might rename the vertices 1=x, 2=y, 3=z, 4=w, for example, to make writing the equations easier (so that they look more like the equations in the text).
  Any questions on those?
Chapter 7: The Joy of x.
- The author begins by lying (unwittingly) to you: "...there won't be any tests this time around." I guess he never thought that anyone would use his book as a textbook!
- Strogatz focuses on x: the variable, that turns arithmetic into algebra. He says that algebra comes in two flavors:
  - "...formulas that ... express elegant patterns about numbers for their own sake." I think of the Fibonacci numbers, ${F(n)=F(n-1)+F(n-2)}$
    for example. (although we've seen that Fibonacci numbers have a lot to do with nature, too); and
  - "...formulas that ... express elegant relationships between numbers in the real world...." I think of the relationship between Fahrenheit and Celsius,
    
    ${F=1.8C+32}$
  Strogatz gives a very personal example: his younger daughter noticed that she would never be able to catch up to her older sister in age (two years older). Strogatz introduces the equation
  
  ${y=x+2}$
  (which we call a linear equation) to express this relationship.
  Age problems can be "a lot of fun": maybe you've seen these before:
  - Here's an easy one: Jo is 2, and her sister Leah is 2 years older. How old is Leah? (We use the one equation above, and another equation -- ${x=2}$ -- to solve this).
  - Here's a trickier one: Today I am four times as old as my sister; in four years I will be twice as old as she. How old am I? (what are the two equations?)
- Now to our question of the day (p. 46). Let's see how many of you got that one right, and how many got that one wrong. Strogatz asserts that people will tend to get it wrong more than they'll get it right.
  The reason people get this wrong is because they confuse an identity with a unit conversion formula. Let's think about why this problem comes about....
- Next is the story of two great physicists, Richard Feynman and Hans Bethe. Let's take a look at the figure on p. 48 which is the subject of the discussion: how to square numbers near 50.
  Note: "near 50" means that x is thought of as small.
  Tricks like this are useful in real life, as Richard found out. Here's another one: conversion to Fahrenheit from Celsius: as already said,
  
  ${F=1.8C+32}$
  But we can use an identity to make that calculation easier, as my brother discovered on our recent trip to Canada (where they, like everyone else in the world, use Celsius for temperature -- the US is alone in our love of the ridiculous "British units" -- even the Brits gave up on them!):
  
  ${F=(2-0.2)C+32}$
  I hope that you'll agree that ${1.8=2-0.2}$ .
  The reason why this formula is easier is because of the operations required to compute. Think of it this way: given C, double it, subtract 10 percent of that, and add 32:
  
  ${F=2.0C-0.2C+32}$
  So
  - What's C=100 in Fahrenheit?
  - What's C=0 in Fahrenheit?
  - What's C=50 in Fahrenheit?
  - What's C=-40 in Fahrenheit?
- Strogatz gives another example of a useful algebraic formula:
  
  ${(1-x)(1+x)=1-x^2}$
  presenting it in the context of the stock market; and he ends with the "icky relationship" formula:
  Your partner in a relationship, where your age is x, should be at least ${\frac{x}{2}+7}$ : so your partner's age y should satisfy
  
  ${y\ge\frac{x}{2}+7}$
  in age. What do you think? Let's look at some example, and compute the range of relationship ages you can consider to be "non-icky".
  You must not be too young for your partner, either: hence
  
  ${x\ge\frac{y}{2}+7}$
  which we can solve for y, to yield
  
  ${y\le{2(x-7)}}$
  Putting them together, we get the "appropriate partner age relationship:"
  
  ${\frac{x}{2}+7\le{y}\le{2(x-7)}}$
  I'm x=52, so my range is
  
  ${33\le{y}\le90}$
  Fortunately my wife falls somewhere in that range....
  1. What's your non-icky relationship range?
  2. At what age do the two ages x and y equal each other?
  3. What range do you get for a 12-year old? In what sense does that make sense?

Website maintained by Andy Long. Comments appreciated.