Day 37, MAT115

Our author says that, while it's true that "you'll find later in life that it's handy to know what a standard deviation is", it is "even handier to know what a distribution is."

So our objective in this unit is to understand three things, actually:

1. A distribution
2. Measures of central tendancy (mean, median)
3. Measures of spread (standard deviation)

1. We collect data;
2. construct a histogram, or graph of the data, grouping the data into "bins"; then
3. attempt to describe the distribution of the data using statistics. Some of the tools we use are
   • A catalog of distributions
   • Measures of central tendancy (mean, median)
   • Measures of spread (standard deviation)

   By "catalog of distributions" I mean some candidates for the model behind the data. We may discover that the data looks symmetric, for example, which would rule out a bunch of types of distributions. If the histogram of the data is bell-shaped, then perhaps it is normally distributed, which is what are author is interested in discussing here.

• The average American has one testicle and one ovary.
• The average income for a Lakeside School (Seattle, Washington) graduate was $2.5 million. (In 1997)

How can we explain these two statistics? Let's start with that first one. Is it true that the average American has one testicle and one ovary? Think about how the average -- or mean -- is defined.

Let's try a different measure of "central tendency":
The median American has no testicles and two ovaries.

Mean and median try to characterize the "middle" of a distribution. Do you know how they're defined?

Why do these values of mean and median make sense? What is the distribution of testicles and ovaries?

• Certainly you've rolled dice.....

  This simulation produces a variety of distributions. What are their properties?

  • One die: a uniform distribution (flat, but symmetric)
  • Two dice: a "tent" distribution (peak, triangular, still symmetric)
  • Six (and, better yet, nine) dice: a distribution which is starting to look very normal.

• Normally distributed data is symmetric -- it's as likely to be above the mean as below the mean.

• Hexstat probability demonstrator (the "Galton board") demonstrates the author's contention that "...the pattern is utterly predictable: it always forms a bell-shaped distribution -- even though it's impossible to predict where any given ball will end up." (p. 177)

  For example, check these out:

  • whoops!
  • that's better....
  • Here's a description of the Hexstat, from the back of the device

• Pascal's Triangle and the normal curve

  This version of Pascal's triangle goes up to the "8 row" (with nine columns); since there are nine "bins" in my Hexstat Probability Generator, the numbers in this version of Pascal's triangle are actually indicative of the probabilities of the balls ending up in any of the bins. So it's 70 times more likely that a ball will end up in the middle bin than in the end bins.

  If you want the actual probabilities of each bin, you divide each values in the triangle by the total for the row (in this case, ).

• Replacing a histogram by a smooth curve....
  

  How is our mathematician doing at modeling the data?

  What has she missed?

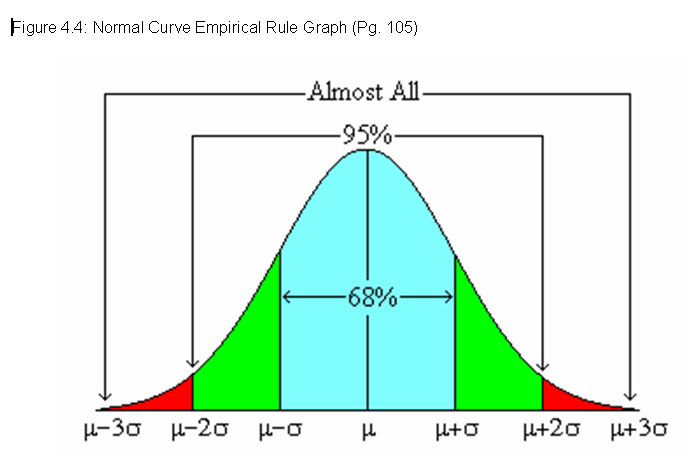
• The greek letter represents the "standard deviation", which is reflective of the spread of the data.

  A deviation is the difference between a data value and the mean value. So if the mean height is 5'10", and you're 5'8" tall, then your deviation is -2. The "standard deviation" thus is a measure of the "typical deviation".

  The larger is, the more spread out the normal curve becomes. It's still bell-shaped -- it's just broader and flatter.

• Percentages in categories, by using as a measuring stick.
• Practical Example
  (We can now answer a few of these questions using the empirical rule.)

• Notice how we're using statistics (in this case a model distribution) to compute probabilities.

Unfortunately people who know a little stats may get infatuated with the normal distribution, and apply it even where it's not appropriate.

• power law distribution of cities (p. 179)
  • This distribution is obviously not normal: it's like the distribution in the comic above. One of the first things you might notice is that it's not symmetric.
  • It's also got a lot more action in the tail than we would expect, which is our authors point.

• Tank Bus #11
  • My daughter is in the early bird program at Highlands, so she takes the early bird bus from home to school.
  • We've been watching the times of the bus, and collected data on three of these cards: And here's the resulting histogram:

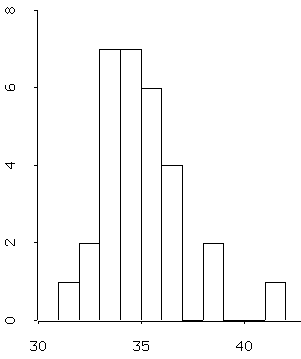
  • The data:
    • minutes from 6:00:
      31 32 32 33 33 33 33 33 33 33 34 34 34 34 34 34 34 35 35 35 35 35 35 36 36 36 36 38 38 41
    • Mean: 34.5
    • Median: 34
    • Standard deviation: 2
    • Check out that maximum value: how many standard deviations away from the mean is it?
    • If the data from this sample reflects a normal distribution with mean 34.5 and standard deviation of 2, then the probability of a 41 or greater is approximately .00023, or less than 3 in 10000.

      Do you believe that this data is normally distributed?

    • If the bus broke down and was really late (e.g. 60), what would happen to the mean and median values? (Mean: 35.1) According to normal probability theory, the probability of this is 0. Do you believe that it's impossible? No? Fat tail!

It and the statistic about Lakeside School are in the same category (Bill Gates and Paul Allen, founders of Microsoft, graduated from Lakeside, which tends to push up the mean), while the median remains unchanged.

In an unfavorable light, Bush's use of the mean could be construed as one of the three lies: "lies, damned lies, and statistics."

Better in both cases to use a median as the measure of central tendancy: