Day 39, MAT115

There's a cool one by the Delta sigma zeta gamma sorority/fraternity, that I saw in the Student Union.

• Curve: add 6 to your raw score (test is out of 50)
• Max: 101
• Min: 25
• Mean: 71.5
• Median: 73
• Standard Deviation: 18
• The Exam
• A Key
• A Grade Histogram

1. Some of you clearly didn't do the reading. I did say that you should do the reading, didn't I? Why then wouldn't one do the reading? Just hoping that I was lying? I could have been lying: but I wasn't lying....
2. Did the extra credit look familiar? I assigned it as a homework exercise. No one got it. Does that mean that no one's doing the homework? These are the questions a professor asks himself, late at night....

   "Why didn't anyone ask about it?" the professor asks himself. What is the answer?

• I'll have the comprehensive final in two parts: new material and old material.
• I'll consider the new material like a separate midterm exam; then I'll take the best three of your four "midterm exams".
• So the final exam can help make up for a stumble along the way. But you will have to do well on the new material!

• Statistics are closely related to probability, which is why they're grouped together in our reading ("Students would be better served by learning more about probability and statistics", p. 175), and which is why we're studying them right after studying probability.

  Our author says that, while it's true that "you'll find later in life that it's handy to know what a standard deviation is", it is "even handier to know what a distribution is."

  So our objective in this unit is to understand three things, actually:

  1. A distribution
  2. Measures of central tendancy (mean, median)
  3. Measures of spread (standard deviation)

• A lot of data exhibit the normal curve - but some data don't!
  • Replacing a histogram by a smooth curve....
    

    How is our mathematician doing at modeling the data?

    What has she missed?

• The Empirical Rule (for normal data)
  
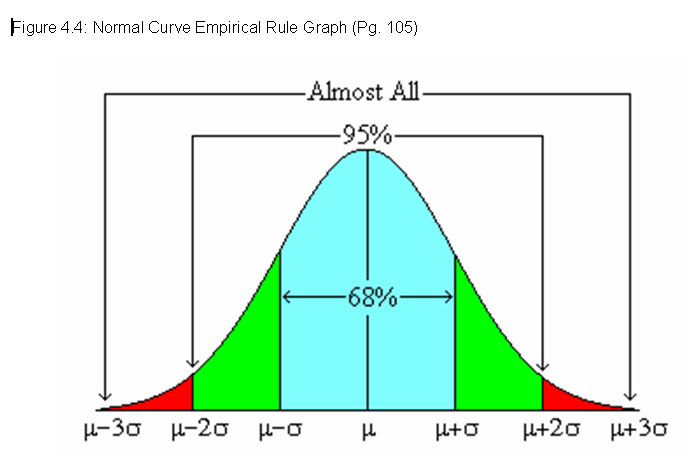
  • The greek letter represents the "standard deviation", which is reflective of the spread of the data.

    A deviation is the difference between a data value and the mean value. So if the mean height is 5'10", and you're 5'8" tall, then your deviation is -2. The "standard deviation" thus is a measure of the "typical deviation".

    The larger is, the more spread out the normal curve becomes. It's still bell-shaped -- it's just broader and flatter.

  • Percentages in categories, by using as a measuring stick.
  • Practical Example
    (We can now answer a few of these questions using the empirical rule.)

  • Notice how we're using statistics (in this case a model distribution) to compute probabilities.

• On page 178, we see that people exaggerate their heights -- this shows up as a shift in the mean, in the position of the middle of the data. Interesting use of statistics, isn't that!

  Notice that it's a little flatter, too. That probably means that some people are honest, and others exaggerate their height even more than two inches. This means that there will be a larger spread (standard deviation) in the heights than one would expect.

  Self-reported data is notoriously dangerous, because of these sorts of biases: everyone wants to be a little taller, so they "make themselves taller"....

• Fat-tailed distributions have more data out in the tails of the distribution than the normal distribution would suggest. They don't follow the Empirical Rule.

  Unfortunately people who know a little stats may get infatuated with the normal distribution, and apply it even where it's not appropriate.

• Examples:
  • power law distribution of cities (p. 179)
    • This distribution is obviously not normal: it's like the distribution in the comic above. One of the first things you might notice is that it's not symmetric.
    • It's also got a lot more action in the tail than we would expect, which is our authors point.

  • Tank Bus #11
    • My daughter is in the early bird program at Highlands, so she takes the early bird bus from home to school.
    • We've been watching the times of the bus, and collected data on three of these cards: And here's the resulting histogram:

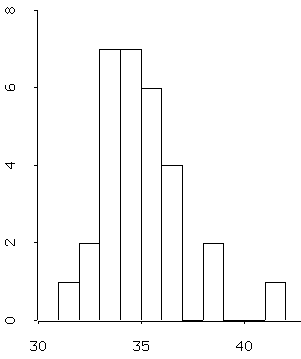
    • The data:
      • minutes from 6:00:
        31 32 32 33 33 33 33 33 33 33 34 34 34 34 34 34 34 35 35 35 35 35 35 36 36 36 36 38 38 41
      • Mean: 34.5
      • Median: 34
      • Standard deviation: 2
      • Check out that maximum value: how many standard deviations away from the mean is it?
      • If the data from this sample reflects a normal distribution with mean 34.5 and standard deviation of 2, then the probability of a 41 or greater is approximately .00023, or less than 3 in 10000.

        Do you believe that this data is normally distributed?

      • If the bus broke down and was really late (e.g. 60), what would happen to the mean and median values? (Mean: 35.1) According to normal probability theory, the probability of this is 0. Do you believe that it's impossible? No? Fat tail!

  • Our Exam 3 histogram: is it fat-tailed?

• Bush's use of the mean versus the median in a fat-tailed distribution (p. 181) could be viewed at its most favorable as "casting something (in this case a tax rebate) in the best light".

  It and the statistic about Lakeside School are in the same category (Bill Gates and Paul Allen, founders of Microsoft, graduated from Lakeside, which tends to push up the mean), while the median remains unchanged.

  In an unfavorable light, Bush's use of the mean could be construed as one of the three lies: "lies, damned lies, and statistics."

  Better in both cases to use a median as the measure of central tendancy: