Day 8, MAT115

Fibonacci "...travelled widely with his father and recognised the enormous advantages of the mathematical systems used in the countries they visited. Fibonacci writes in his famous book Liber abaci (1202):-

When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it, for whatever was studied by the art in Egypt, Syria, Greece, Sicily and Provence, in all its various forms.

Here is that rabbit problem from the Liber abaci:

A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?

This is the situation:

• Start with a new-born pair of "immortal" bunnies (they never die).
• A new-born pair requires a month to mature.
• The following month, the pair produces a new pair, which is subject to the same rules.
• Do it again, do it again, do it again!

---

But, before we go on, a card trick! Today I will be able to read the mind of my lovely assistant and tell what card he or she is hiding from me.

• LA takes 5 cards.
• LA turns one card down.
• The LA then places the cards in any order they choose.
• By their actions and body language, I can determine the hidden card!

How do I do it?

---

Fibonacci number decomposition and Fibonacci Nim.

• We looked at some special cases, and what did we conclude?

  We concluded that, if the starting number was a Fibonacci number, then it was best to go second (be player 2); if not Fibonacci, try to be player 1.

• What's the winning strategy in Fibonacci Nim?

  We concluded that it comes down to this fact:

  Every natural number is either

  1. Fibonacci, or
  2. can be written as a sum of non-consecutive Fibonacci's in a unique way.

  So winning comes down to two things:

  • If at any time you can apply the following strategy, you are guaranteed to win:

    Write the number of counters as a sum of non-consecutive Fibonacci numbers, and take the smallest in the sum.

  • If the number of counters starts as a non-Fibonacci (more common), try to go first. Otherwise, if Fibonacci, go second if you can. Then you're in the driver's seat, and you will win.

    If you're in the wrong seat, then use the slow-down strategy: take 1 each time. Eventually your opponent will screw up, and you'll take over the driver's seat!

  Let's look at how a few examples should go: suppose that the number of counters is
  • 26
  • 34
  • 98
  Would you rather be player 1 or 2? What would be the first few moves in a game played by people who both know what they're doing?

How Fibonacci numbers are defined: The Fibonacci numbers are given as a recurrence relation (do it again, do it again, do it again!).

Fibonacci Numbers and Nature:

• From the link above:

  The English puzzlist, Henry E Dudeney (1857 - 1930, pronounced Dude-knee) wrote several excellent books of puzzles (see after this section). In one of them he adapts Fibonacci's Rabbits to cows, making the problem more realistic in the way we observed above. He gets round the problems by noticing that really, it is only the females that are interesting - er - I mean the number of females!

  He changes months into years and rabbits into bulls (male) and cows (females) in problem 175 in his book 536 puzzles and Curious Problems (1967, Souvenir press):

  If a cow produces its first she-calf at age two years and after that produces another single she-calf every year, how many she-calves are there after 12 years, assuming none die?

  This is a better simplification of the problem and quite realistic now.

• dandelions (Here's a scanned dandelion -- a scandelion)
• Spirals in daisies:
  • 21 spirals
  • 34 spirals
  • together
• Similar things happen in artichokes, pineapples, etc. I used to have a cholla cactus skeleton that shows Fibonacci spirals....

• Let's look at some pine cones....

Why does it happen? Some folks believe that it's because of the way things grow, suggesting something like this.

Let's revisit Pascal's triangle, and discover Fibonacci numbers therein:

As usual, the "Fibonacci numbers" were known before Fibonacci, e.g. by the Indians (of Asia):

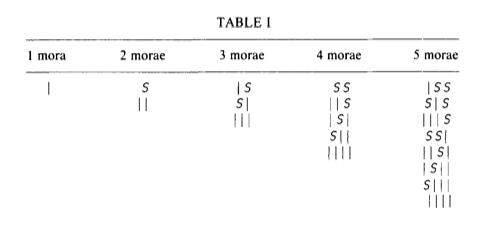
Variations of two earlier meters [is the variation] of a matra-vitta. For example, for [a meter of] three [morae], variations of two earlier meters, one and two, being mixed three happens.
For [a meter of] four [morae], variations of meters of two morae [and] of three morae being mixed, five happens.
For [a meter of] five [morae], variations of two earlier [meters] of three morae [and] of four morae, being mixed, eight is obtained.
In this way, for [a meter of] six morae, [variations] of four morae [and] of five morae being mixed, thirteen happens. And like that, variations of two earlier meters being mixed, [variations of a meter of] seven morae [is] twenty-one.
In this way, the process should be followed in all matra-vittas. [Velankar, 1962; circa 1134CE]

As we move toward the so-called "golden mean" and "golden rectangle", we'll start with a nice logarithmic spiral (see this site)