- You have a homework due next time.
- I've assigned a new homework, due next Thursday.
- Last time we talked about spirals -- Fibonacci and Golden. What questions
do you have?
- We discovered that the Fibonacci spiral leads to rectangles that tend toward a common side ratio of about 1.618....
- The Golden Rectangle, defined by the Greeks, has a side ratio of
$\frac{1+\sqrt{5}}{2} \approx 1.618$ called the golden ratio.While the Fibonacci spirals were created by attaching squares, the golden rectangle was created by removing squares:
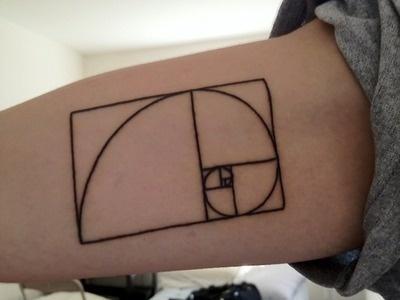

Both had roughly the same effect, however.
I described each of these as an example of a fractal process: a simple rule, applied recursively (that is, do it again, and again, and again!). We believe that nature loves fractals, and we'll study them in more detail down the road.
- Now, back to Pascal's triangle. Let's look a little further into it. In
particular, we note that it contains the Fibonacci numbers:
- Use the hexagonal paper to create a version of the Pascal triangle.
- Now let's find those Fibonaccis....
- I want to push a little harder, however: what do we put in all the empty
hexagons? What if we wanted to fill them, respecting what we know about how
Pascal's triangle is created?
Warning: there is not necessarily a unique way to do so! More on that in a moment. (Remember how fond mathematicians are of uniqueness...!)
- So we find all kinds of numbers in Pascal. But what's Pascal's triangle all
about? Why was it created?
- First of all, one of your readings (p. 128) gives us a
bit of the history of "Pascal's" triangle, studied as far back
as the 5th-3rd century BC in India -- that we know of!
- Pascal used "his" triangle to compute probabilities. It turns out
that it's very useful for counting things.
Blaise Pascal and Pierre de Fermat were working on "Number Theory"
together.
- Pascal's triangle is useful for counting the ways of
combining terms in the expression
$(a+b)^n$
So, for example,
$(a+b)^3=1a^3+3a^2b+3ab^2+1b^3$
(see p. 128, the binomial theorem)
You'll notice that the coefficients of the terms are the numbers from one row in Pascal's triangle.
- First of all, one of your readings (p. 128) gives us a
bit of the history of "Pascal's" triangle, studied as far back
as the 5th-3rd century BC in India -- that we know of!
- Now let's look at an example of how we can use Pascal. Consider the
concept of simple graphs, which I'll present in the context of Facebook. A
simple graph is made up of
- vertices (or points, which we will think of as people), and
- edges (which are also called arcs, connecting two points -- which we will think of as friendships).
Now, if we don't care about "who's who", then we can see all the different types of Facebooks we can have:
- Let's look at some simple cases: 2 or 3 individuals
- All simple graphs with four vertices.
- All simple graphs with five vertices.
- Now, if we add names to the "vertices", then we have more
Facebooks. If everyone's friends with everyone else, then the graphs we
can get will look like this:
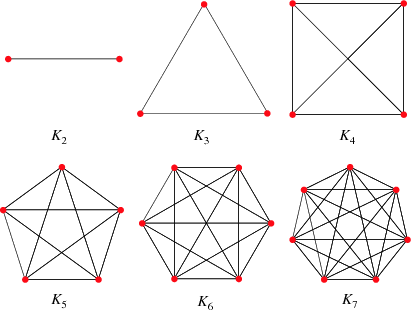
Now how many different Facebook configurations are there for, say
- $K_2$?
- $K_3$?
- $K_4$?