- Your symmetry homework is returned.
- Some of you are struggling. We'll go over the handout....
- Some of you didn't think to do the top part of the third page, so I dropped two points from the total. If you did it, you got a bonus; otherwise, it shouldn't hurt you.
- I got a few face/symmetries to share....
- Some of you are struggling. We'll go over the handout....
- Your Platonic homework is due.
- We have a test coming up next week, Thursday. It will cover the following topics:
- Fibonaccis and the golden mean
- Fibonacci spiral
- Golden rectangle
- More on Pascal's triangle (and extensions like "Leibniz's hexacomb")
- Egyptian multiplication
- Egyptian division
- Symmetry
- Platonic solids
Question of the Day:
Let's review what we learned last time, and finish off the background. Then we'll start in on some applications.
- The Bridges
of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly once?"
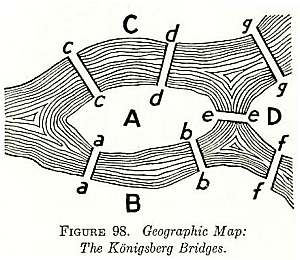

- Solved by Euler
(1735), the beginning of graph theory.
- Graphs are made up of vertices (points) and edges
that connect the vertices. More formally, a graph is defined as
- A collection of points, called vertices.
- A collection of edges, each of which connects two vertices.
- a set of rules, one for each edge, telling how each edge is connected to its pair of vertices.
- The degree of a vertex is the number of edges coming into it.
- Graphs are made up of vertices (points) and edges
that connect the vertices. More formally, a graph is defined as
- Euler's solution:
- Konigsberg: To be traversable, there must be at most two vertices of odd degree.
- Euler noticed the hand-shaking theorem: in any graph, the number of vertices with odd degree must be even.
- An alternative
solution -- thanks to spiked math
- Which of the Platonic solid graphs can be traversed without backtracking (i.e., have an Euler path)? (here they are).
- Solved by Euler
(1735), the beginning of graph theory.
- You've
probably been making graphs for a long time.... (the pentagram)
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
- Exercise: draw all the simple graphs with three
vertices. (We've done this before, when we were talking about Facebooks....)
- A cycle is a route from a node back to itself that doesn't retrace steps.
- One of these graphs is a tree: a graph that has no cycles.
- Where have we seen trees used before?
- Duality -- again!
- Exercise: draw all the simple graphs with four vertices.
- Have you ever seen any of these before? Could we give any of them names?
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
- Exercise: draw all the simple graphs with three
vertices. (We've done this before, when we were talking about Facebooks....)
- Planar graphs are graphs that can be drawn such that no two edges
intersect. Every Platonic
graph can be drawn this way, so they are planar graphs.
- We can show that the complete graph with four vertices is
planar.
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
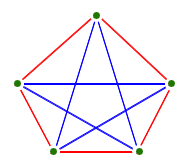
Why is the five vertex graph different? What happens?
- The three utilities and three houses graph is not planar:

- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:

- We can show that the complete graph with four vertices is
planar.
- One focus of this reading is negative numbers. It
was the Indians (of Asia) who put negative numbers on a
firm foundation (as well as zero), in about the 6th
century AD.
"...you can't see negative 4 cookies and you certainly can't eat them -- but you can think about them...." ("and you have to", says our author).
- One of the confusing aspects of negative numbers
from Strogatz's perspective is that the product of two
negative numbers is a positive number.
- But then Strogatz goes on to use the context of
social interactions (negative and positive) to discuss
how we maintain stable relationships.
And the key to understanding stability in three-way social relationships is that the product of two interactions (signified by either +1 or -1) must be equal to the other: so that if two legs are positive, the third in the triangle must be positive; if one leg positive, and the other negative, then the third leg must be negative as well.
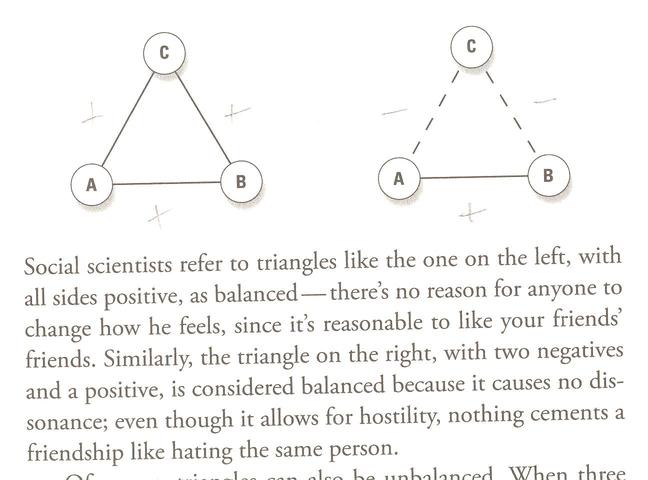
Strogatz sums up the second case above in the familiar saying that "The enemy of my enemy is my friend".
The following (two) graphs are unbalanced:
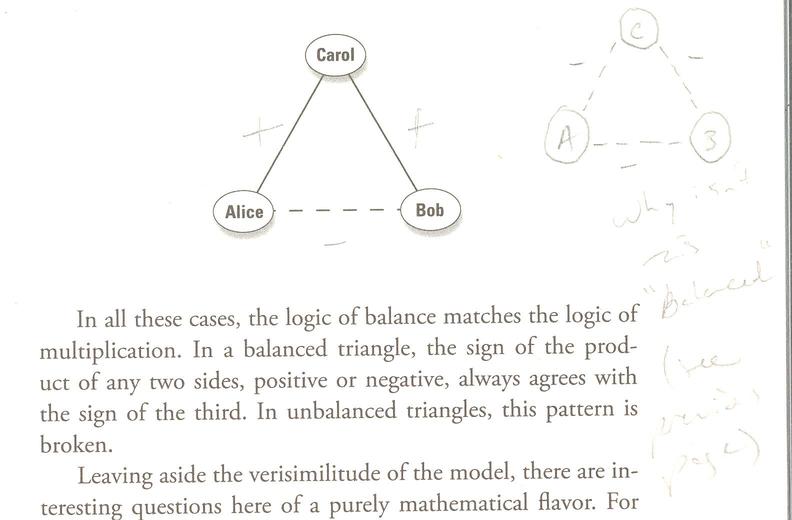
Finally Strogatz shows how historical relationships settled down into this pattern of stability: in "...the run-up to World War I. The diagram that follows shows the shifting alliances among Great Britain, France, Russia, Italy, Germany, and Austria-Hungary between 1872 and 1907."
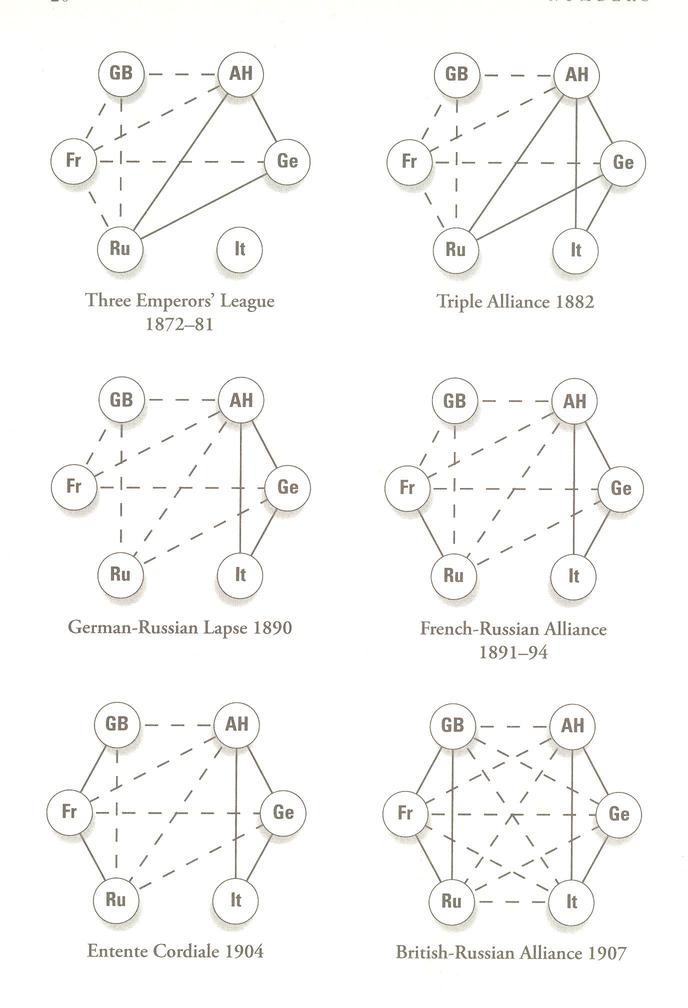
The bottom right graph (complete!) is the only stable configuration, "...balanced, but on the brink of war."
How do we know that it's non-planar?
This section describes how Google uses the "PageRank" algorithm to determine the importance of a webpage (and hence where it falls in the search results for a particular topic).
Graphs provide a useful way of illustrating how pages interact. If there's a link between two pages, then a directed arrow indicates it. Here's the graph of the "toy web" Strogatz considers, with the final rankings:
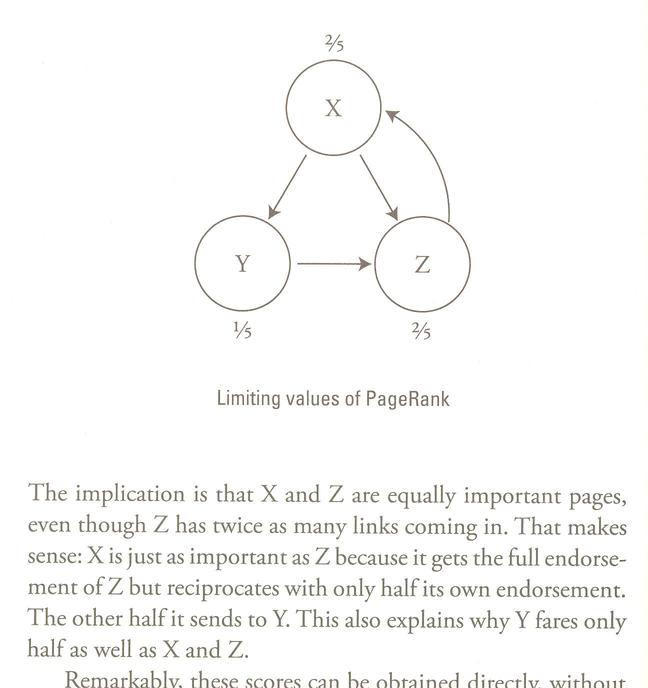
He justifies this ranking in a series of graphs, and a set of equations on page 195. Let's see how these equations work (we'll use this Excel spreadsheet).
Notice that I've written the equations with an index, ,
rather than with the primes. That's because we keep updating
the values to get them at the
stage, and we update based on the previous stage's (
)
values.
We just "do it again", over and over....
This strange algebra is from the field of mathematics called "linear algebra".
In this reading, we discover how to rotate and flip our mattress over the course of the year, so that the mattress gets even wear (while avoiding having to flip the mattress end-over-end the long way -- the "death-defying vertical flip").
"Spin in the spring, flip in the fall" is what some manufacturers suggest.
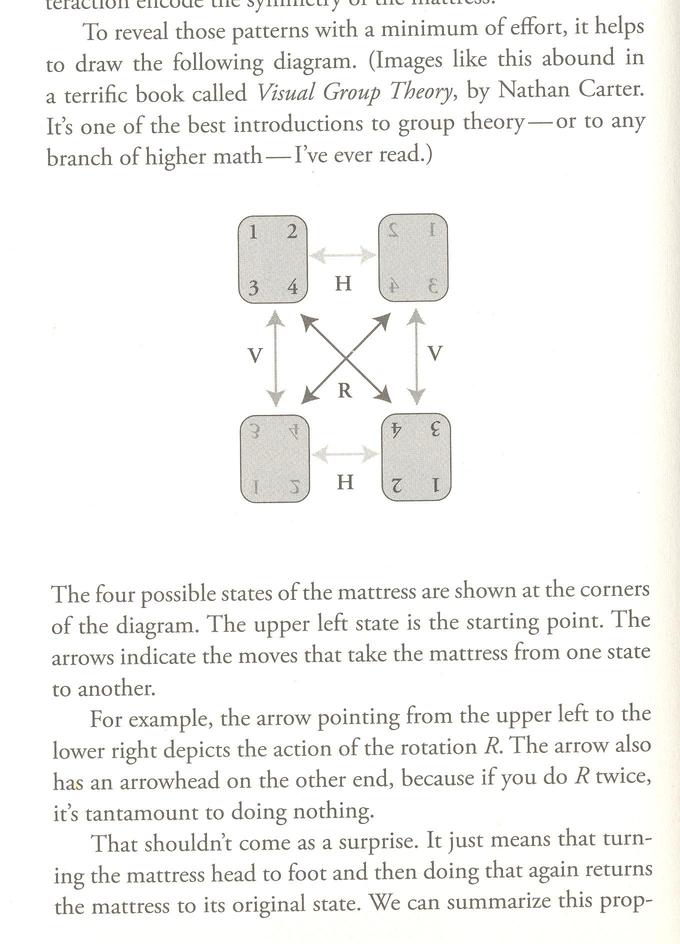
There is a certain amount of curious algebra here:
means that a horizontal flip followed by a rotation is equivalent to a vertical flip. Using only horizontal flips and rotations, we can achieve each of the four possible configurations of a matress. So over the course of two years, you'll have visited all four configurations of your mattress. Bon Nuit!