MAT115 Tree Terminology
NB: in the tree world, we'll frequently use the word "node" rather than
"vertex". They're synonyms, after all, but it's one syllable instead of two,
and mathematicians are notoriously lazy!:)
- tree: an acyclic, connected graph with one specially
designated vertex (or "node") called the root node.
"Acyclic" means that there are no cycles.
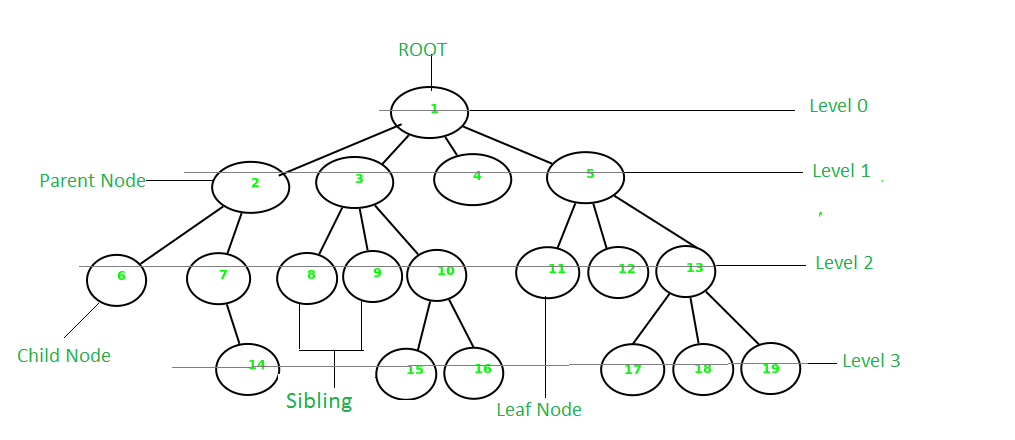
- parent node: the node adjacent to a given node on the path to the
root node
Node 2 is the parent of nodes 6 and 7.
- child node: a node adjacent to a node (its parent) which is closer
to the root node
Nodes 6 and 7 are the children of node 2.
- siblings: nodes sharing the same parent.
Nodes 6 and 7 are siblings.
- internal node: a node with a child
Node 2 is internal, as a parent.
- leaf node: a childless node
Node 6 is a leaf.
- depth of a node: the length of the path from the node to the root
Node 6 is at depth 2.
- depth (or height!) of the tree: the maximum node depth
This tree has depth 3.
- binary tree: a tree in which a root node has at most two children
but no parent, each internal node has a single parent and at most two
children, and leaf nodes have a single parent but no children.
This tree is not binary; it's called "ternary", because parents have at
most three children!
Here's a binary tree:
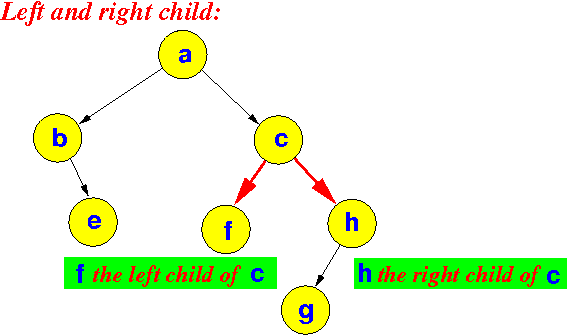
- left child: the node to the left of the parent in a binary tree
- right child: the node to the right of the parent in a binary tree
- perfect binary tree : all leaf nodes are of equal depth, and all parents have two children:
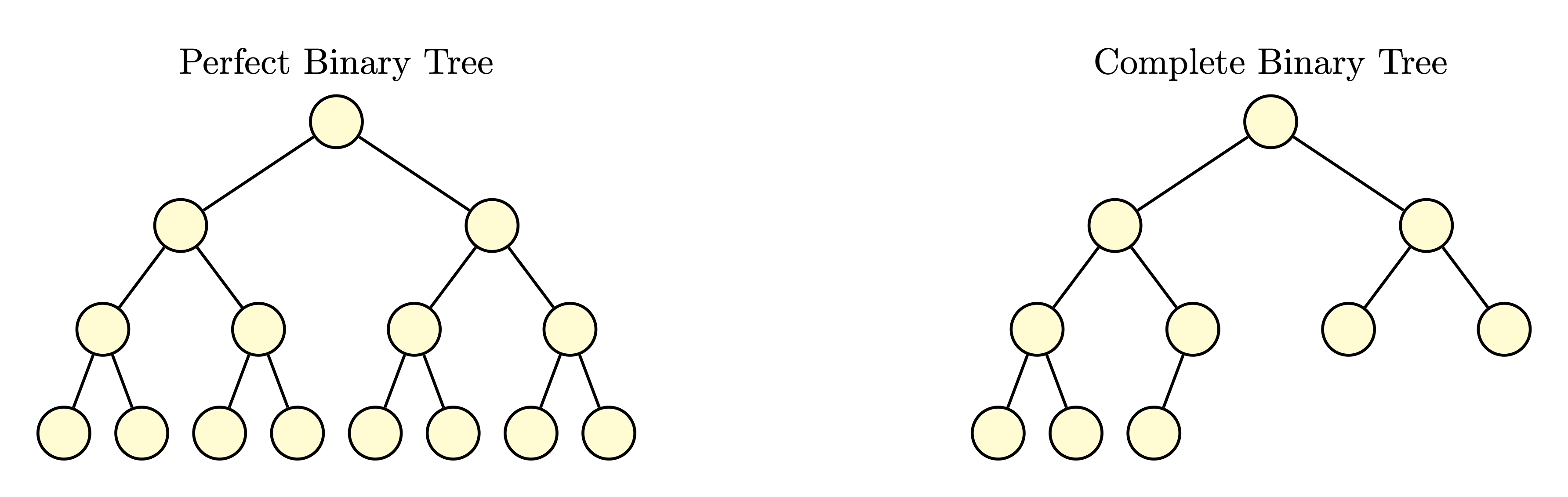
- complete binary tree: an almost-full binary tree (all leaves are of
depth n or n-1, where n is the depth of the tree).
- forest: a bunch of trees (of course! Geez, ask a silly
question....)
Website maintained by Andy Long.
Comments appreciated.


