- Our quiz Thursday will be over our reading Early Concepts
of Number and Counting, and about primitive counting
(turning numbers into strings of zeros and ones, and vice
versa); and the Fraudini trick.
I may put a throwback problem from primes on there, too, because we're struggling with those and need to distinguish the prime from the binary stuff....
- we saw why counting by partition works, and why the mind-reading
of the Great Fraudini works: because of the
Binary Factorization Theorem: Every counting number is either a power of 2, or can be written as a sum of distinct powers of 2 in a unique way.
- There is a one-to-one correspondence between the counting numbers
and the sums of distinct powers of 2.
The fact that it's a one-to-one correspondence is what the "unique" part means; the fact that we say "distinct" powers of 2 means that you can't do this: \[ 5 = 4 + 1 = 2 + 2 + 1 \] In the second case, the sum doesn't feature distinct powers of 2: some repeat.
Here are the first few powers of 2 (note that 1 is a power of 2: \(2^0\)):
\[ \begin{array}{l} 2^0 = 1 \cr 2^1 = 2 \cr 2^2 = 4 \cr 2^3 = 8 \cr 2^4 = 16 \cr 2^5 = 32 \cr 2^6 = 64 \cr 2^7 = 128 \cr 2^8 = 256 \end{array} \]
They go on forever, of course! Turns out you can represent any number using powers of two, "base 2" -- in fact, that's what computers do.
- So we then practiced our Fraudini and binary factorization skills: you should
know how to
- do the Fraudini trick, using the six cards which construct
any number from 1 through 63.
We can carry out the "Fraudini process" using a binary tree, like we're cashiers making change -- just using funny bills, i.e. 1, 2, 4, 8, 16, and 32.
And you can only use one bill of each type when you make change. So 57=32+16+8+1, for example: 111001.
- write a number (in our base, base 10) as a binary
number (using only the powers of 2).
I've written out the first four Fraudini cards when you're only able to read numbers up to 15, and we'll have a look at those -- in both base 10, and in binary.
The binary representation makes it clearer why the trick works....
- do primitive counting, by partitioning the
given set of objects into "halves", keeping track of
whether there is an object left over, or not.
If written down as we've done in class, this results in the writing of the binary representation of a number.
We can use ternary trees to carry out this process: remember to use your "turkey feet" to create the three branches of the ternary tree.
- recover the "base 10" number, if given its expression in binary.
- do the Fraudini trick, using the six cards which construct
any number from 1 through 63.
- We watched Vi Hart doing a binary
hand dance.
Vi Hart has the most amazing ways of showing us interesting mathematics. She shows us that we can count to 31 on one hand. And, if you'll use the 10 fingers of two hands, you can get all the way up to $2^{10}-1=1023$, instead of just $2^{5}-1=31$.
Some people can only count to 10 with their fingers....
Today's Question of the Day:
(and what can we learn from it? what does it do for us?)
- Permit me to begin with a brief summary of the number six, however, to show where we are at this point.
- Today's new thing, the best new thing in the world, is an old
thing. It's called "Yang Hui's triangle", and you should study it
carefully:
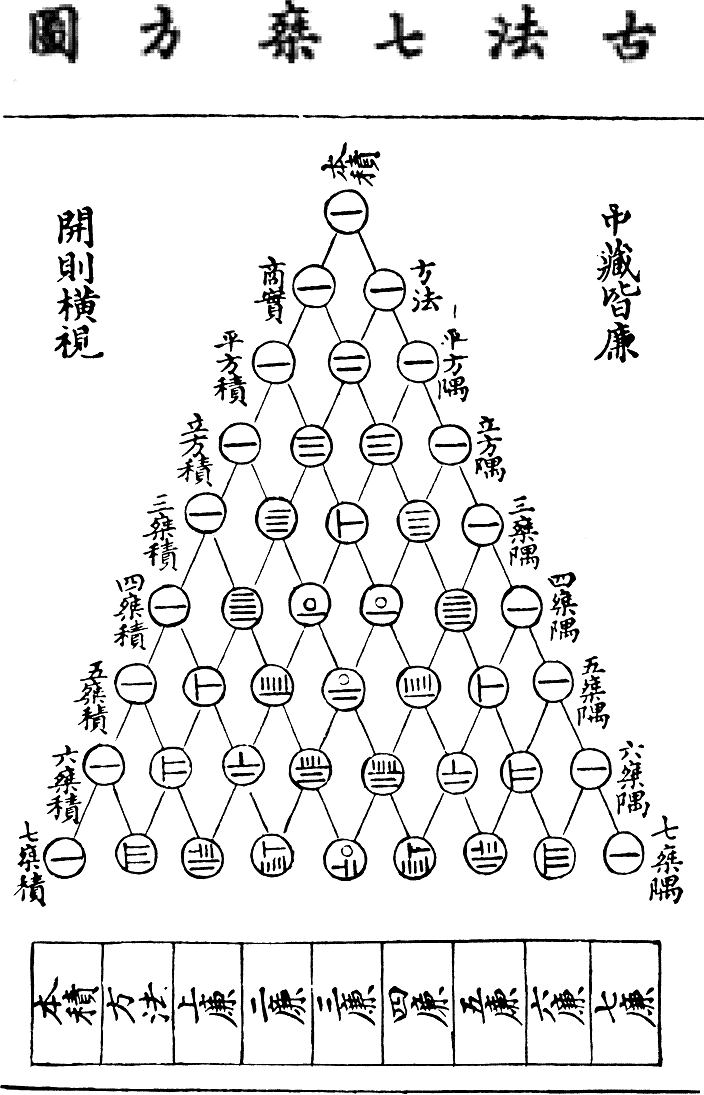
Let's try to answer some questions: Mathematicians look for patterns.
- What do you notice? What catches your attention?
- Can you understand the writing system for numbers?
- Can you find any number patterns?
- What is this thing? What is its purpose?
- There's an error in the table....
- When we're done with those questions, we're going to create a more modern version of
this triangle on the back of your sheet.
There's a rule that we want to decipher for this triangle; and we'll relate it to counting.
For example, Pascal used it to answer this question:
What are the chances that a family of X children will have Y girls?
Before we can do that, however, we need to recognize some features of the table.
- The resulting triangle contains some interesting number patterns:
- The counting numbers (natural numbers)
- Triangular numbers
- Tetrahedral numbers (next time)
- The powers of two....
- (And more! Your reading comments on all of these... and more!)
- American Bandstand dances to Gimme Some Lovin', a hit by The Spencer Davis Group: here's their version.
- List of musical works in unusual time signatures
- Blue Rondo a
la Turk, by Dave Brubeck: illustrating
how to play a piece in 9/8.
Watch Dave Brubeck's leg, counting out the rhythm....