- Our quiz
- The quiz and key: let's talk about it!
- Median: 7
- There's still a fair amount of confusion about prime numbers. What questions do you have?
- After the quiz someone said that they didn't think that
I'd be so specific in the reading, asking about what a
particular group of people did (e.g. the South
Africans).
I replied "Well, it was a homework question," and the student said "We have homework?!"
Whoops! Yes, you have homework. You can access this off our homepage, under "Schedule and Assignments".
- We summarized Yang Hui's triangle, and recalled some of the
secrets of this ancient mathematical document (from about 1200 AD)
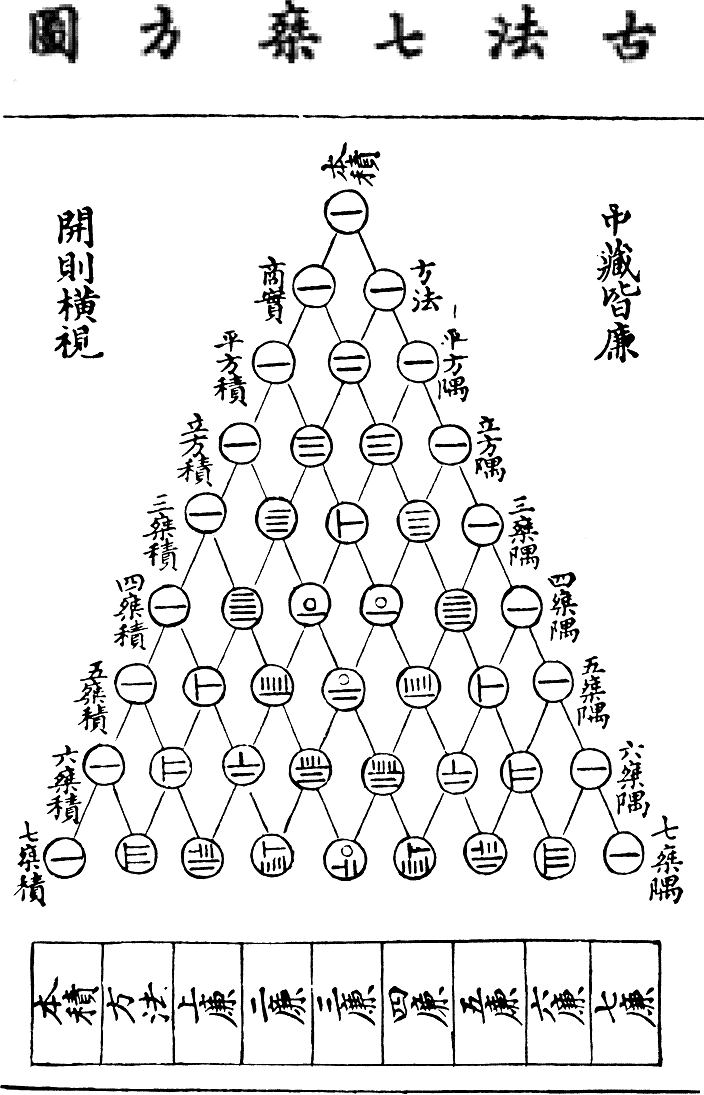
and that it's more generally called Pascal's triangle today (after Blaise Pascal, who studied it to death!).
- We spent most of the rest of the class making connections between
- the number of ways of choosing members from a set (thinking of them as vertices on a complete graph)
- The entries in rows of Pascal's triangle
- We went through the first five complete graphs, linking them to Pascal's triangle, and then
- I tried to show how \(K_6\) was created from the "row above" (the row for \(K_5\)).
- We checked out a third
version of the triangle, and noticed some things suggestive of our number systems.
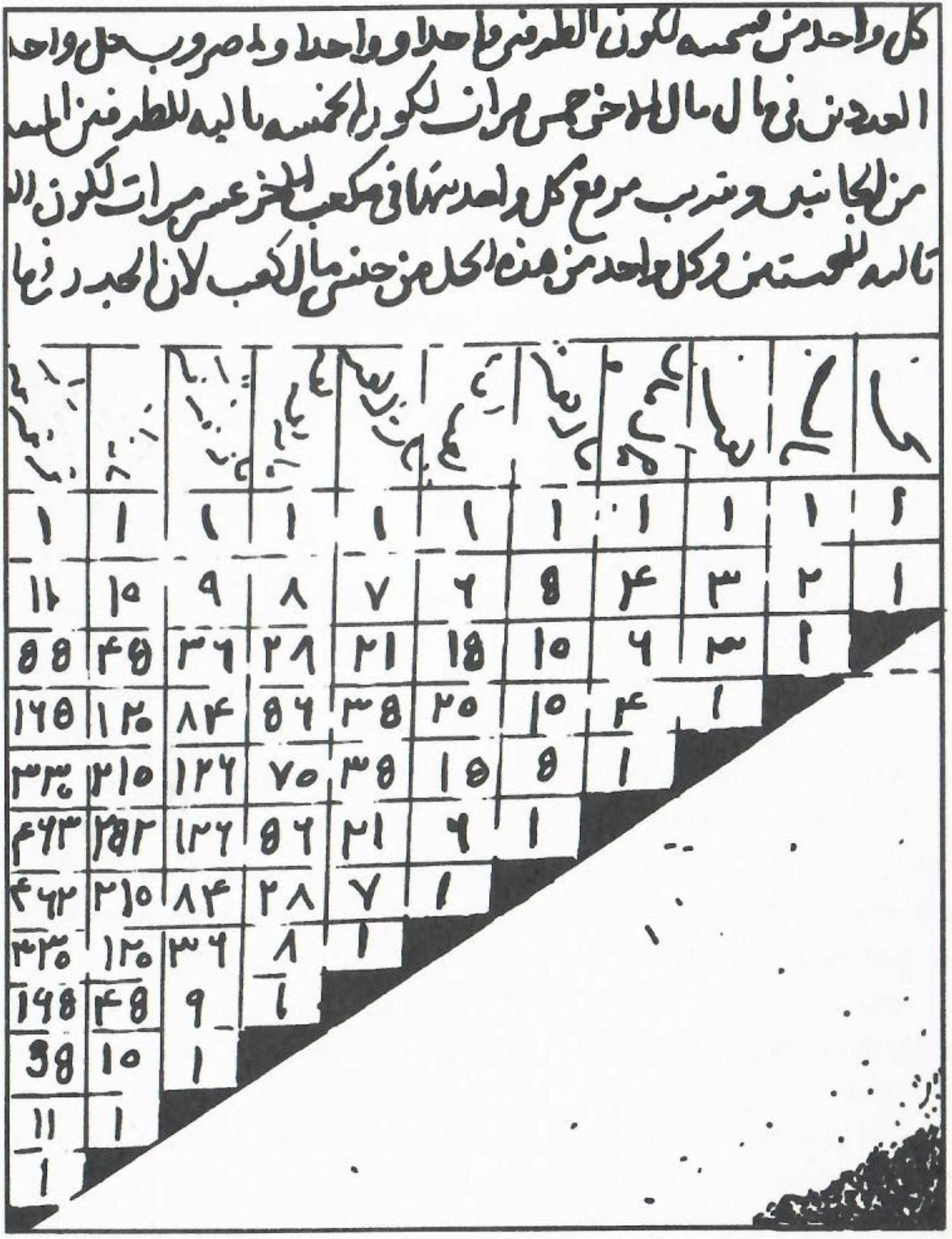
Question of the Day:
-
Today this triangle is generally called "Pascal's Triangle", after Blaise
Pascal, in part because he studied it so thoroughly, and published
a paper with many of its properties; he and Pierre de Fermat were
working on the foundations of probability and statistics together, and
found it singularly useful.
Pascal used "his" triangle to compute probabilities, in part because of his interest in gaming and gambling. It turns out that this "arithmetic triangle" (as he called it) is very useful for counting things.
- Now let's take a look at how we can use Pascal in the study of
graphs. Consider the concept of simple graphs, which I'll
present in the context of Facebook.
Definition: A simple graph is a graph without loops, and never more than one arc connecting any two vertices (friendship is a binary thing: it either exists or it doesn't; and you're not friends with yourself).
It turns out that Pascal's triangle gives all the ways of having a "Facebook" for any number of individual (distinct) people.- vertices (or points, which we will think of as the people), and
- edges (which are also called arcs, connecting two points -- which we will think of as friendships).
Now, if each vertex represents a unique individual (we name them), then Pascal's triangle tells us all the different Facebooks possible, of each type. If everyone's friends with everyone else, then the graphs we can get will look like these, the complete graphs:
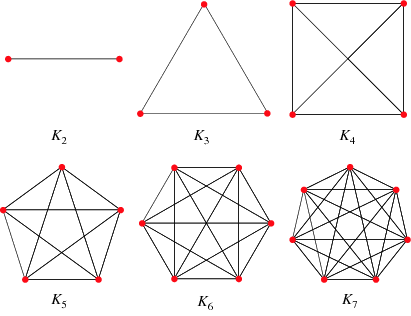
Now how many different Facebook configurations are there for, say
- 1 individual
- 2 individuals
- 3 individuals, with two friendships?
- 4 individuals, with three friendships?
Each choice of a different set of friendships results in a different Facebook. So we begin by asking how many arcs X are possible, and then asking how many ways can we pick Y arcs from X?
How do we use Pascal's triangle to find the answer for a given number of people? We first find the number of arcs for the given number of people (the appropriate triangular number), and then read off the number of different ways of having a given number of Facebook friendships from the "arc row" of the table.
So if there are 6 arcs (as there are for \(K_4\)), we look at the "6" row, and we can read off the number of ways of having 0, 1, 2, 3, 4, 5, and 6 friendships; and we can calculate probabilities of any particular type, if we were to select a type at random, by dividing by all the possible ways of selecting. This is given by the appropriate power of 2: \(2^6=64\) in this case since we're in the 6th row.
The same process works if we want to decide questions like Pascal's about boys and girls, such as
You have four extra tickets to a concert; in how many ways could you choose a set of four friends from your seven favorite friends? (Notice that it's the same number of ways as the number of ways of excluding three friends: the table is symmetric!)
There is actually a formula for computing the entry in any row of Pascal's triangle. Note that we count the entries across a row starting from 0 (choose 0, choose 1, ..., choose \(n\))
It's represented in different ways, but my favorite is \[ C^n_p = \frac{n!}{p!(n-p)!} \] (because these entries are called combinations); another common notation is \[ {n \choose p} \]
(and we say "\(n\) choose \(p\)").
That's a daunting formula! So let's see how it works. That exclamation point (!) means to multiply all the natural numbers from \(n\) down to 1. So \(6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\). We define \(1! = 1\).
Oddly enough, we also define \(0! = 1\). That should just tell you that mathematicians have very odd senses of humor.
The triangular numbers are what we get from "choosing 2": \[ C^n_2 = \frac{n!}{2!(n-2)!} = \frac{n \cdot (n-1) \cdot (n-2) \cdot (n-3) \ldots \cdot 2 \cdot 1}{2!(n-2) \cdot (n-3) \ldots \cdot 2 \cdot 1} \] so there's a whole bunch of cancellation, and
\[ C^n_2 = \frac{n!}{2!(n-2)!} = \frac{n \cdot (n-1)}{2!} = \frac{n \cdot (n-1)}{2!} \]
These are the triangular numbers: plugging in 2, 3, 4, 5, and 6 for \(n\), we get the usual suspects: \[ \begin{array}{c} C^2_2 = 1\cr C^3_2 = 3\cr C^4_2 = 6\cr C^5_2 = 10\cr C^6_2 = 15 \end{array} \]
- Pascal's triangle is useful for counting the ways of
combining terms in the "algebraic expression" (called a "binomial")
\[ (a+b)^n \]
So, for example,
\[ (a+b)^0=1 \] \[ (a+b)^1=1a+1b \] \[ (a+b)^2=1a^2+2ab+1b^2 \] \[ (a+b)^3=1a^3+3a^2b+3ab^2+1b^3 \] \[ (a+b)^4=1a^4+4a^3b+6a^2b^2+4ab^3+1b^4 \]
(see your assigned reading).
I hope that you noticed Pascal's triangle peeking out from the right hand sides above!
Do you remember that the Chinese translation of Yang Hui's triangle has the words "to the 4th power" (etc.) in it? These are the powers, of these "binomials".
-
What this allows us to do is calculate the probabilities of
a lot of different events. For example, suppose you wonder
about the probabilities of rolling a six on four rolls of a die.
If it's a fair six-sided die, the probability of rolling a six is 1/6. The probability of rolling a six is \(a=1/6\); then the probability that you don't roll a six is \(b=5/6\).
Let's roll four time:
\[ (a+b)^4=1a^4+4a^3b+6a^2b^2+4ab^3+1b^4 \] Then \[ (\frac{1}{6}+\frac{5}{6})^4=1\left(\frac{1}{6}\right)^4+4\left(\frac{1}{6}\right)^3\left(\frac{5}{6}\right)+6\left(\frac{1}{6}\right)^2\left(\frac{5}{6}\right)^2+4\left(\frac{1}{6}\right)\left(\frac{5}{6}\right)^3+1\left(\frac{5}{6}\right)^4 \]
Since every denominator has a \(6^4=1296\) in it, we can re-write the probabilities in perhaps a more intuitive way. (In class)
-
We can calculate the probabilities of more interesting
situations.
For example, suppose that the probability that you have a cold on a given winter day is \(a=1/100\); then the probability that you don't have a cold is \(b=99/100\).
Let's suppose that winter is 90 days long. What is the probability that you have a cold-free winter? We need to compute the 90th row in the table, which has some really big numbers!
\[ \left(\frac{1}{100}+\frac{99}{100}\right)^{90} \]
- Probability of a cold-free winter: \[ 1\left(\frac{99}{100}\right)^{90} \approx 0.4047 \]
- Probability of a one-day cold winter: \[ 90\left(\frac{1}{100}\right)^1 \left(\frac{99}{100}\right)^{89} \approx 0.3679 \]
- Probability of a two-day cold winter (uh oh, we
need the rest of the 90th row of the triangle!:):
\[
4005\left(\frac{1}{100}\right)^2 \left(\frac{99}{100}\right)^{88} \approx 0.1654
\]
If you're wondering where that 4005 comes from, it's the triangular entry of the 90th row of Pascal's triangle (third entry from the left, choosing 2): \[ C^{90}_2 = \frac{90!}{2!88!} = \frac{90 \cdot 89}{2} = 4005 \]
- Probability of a three-day cold winter:
\[
117480\left(\frac{1}{100}\right)^3 \left(\frac{99}{100}\right)^{87} \approx 0.0490
\]
The tetrahedral entry of the 90th row of Pascal's triangle: \[ C^{90}_3 = \frac{90!}{3!87!} = \frac{90 \cdot 89 \cdot 88}{3 \cdot 2} = 117480 \]
- etc.
- Hexagonal Paper
- Pascal's triangle (wikipedia)
- American Bandstand dances to Gimme Some Lovin', a hit by The Spencer Davis Group: here's their version.
- List of musical works in unusual time signatures
- Blue Rondo a
la Turk, by Dave Brubeck: illustrating
how to play a piece in 9/8.
Watch Dave Brubeck's leg, counting out the rhythm....