Day 12, MAT115R

• Our quiz is returned
  • Median: 7
  • The key
  • Some comments:
    • It would pay to go back over agendas, to make sure that you remember the things that we've been doing prior to the quiz.

      For example, some of you didn't have a thing to say about Yang Hui's triangle (which figured prominently in the agendas). That spells trouble....

    • I was suprised that some of you couldn't generate Pascal's triangle. You'll need to be able to do that.

    • I don't recall that anyone mentioned the error in Yang Hui's triangle: did anyone? Symmetry pointed to that error.

• We discussed the factorial function, and how it represents the number of permutations of \(n\) objects: ways of representing \(n\) objects where order counts.

  So in how many ways can we write order six things?

  \(6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\).

  For combinations, order doesn't count: we're just choosing \(p\) things from \(n\) things.

• Then we addressed the question "How did Egyptians do their division?" It's much like Egyptian multiplication, but you do have in introduce the f-word, "fractions".

  We saw the parallels between multiplying 23*42 and dividing 966 by 42.

  23=16+4+2+1

  1 42 * 2 84 * 4 168 * 8 336 16 672 * 32 Too big!

  672+168+84+42 = 966

  • We then started with the easy ones -- where one number is actually evenly divisible by another.

    For example divide 40 by 8:

    1	8
    2	16
    4	32

    So the answer is 5 (how do we get 5?)

  • Now: what happens when the division doesn't work out quite so nicely? We get "the f-word": fractions!

    • When the denominator doesn't divide the numerator evenly, fractions make it more interesting (my word -- you might use a different word!:).

      Let's look at an example: divide 35 by 8.

      In a way we turn it into a multiplication problem: what times 8 equals 35? So we know the 8, and use it to "double" -- but then to "halve", when 8 won't go evenly into 35:

      1	8
      2	16
      4	32
      1/2	4
      1/4	2
      1/8	1

      So the answer is 4+1/4+1/8

    • the Egyptians restricted themselves to the so-called "unit fractions", which are fractions of the form 1/m: unit fraction table, which is found on the Rhind Papyrus (which dates to around 1650 BCE).

      But they didn't restrict themselves to "halving", as our next example shows (in which they also "seventh"ed -- then they doubled that!).

      Divide 6 by 7:

      1	7
      1/2	3+1/2
      1/4	1+1/2+1/4
      1/7	1
      1/14	1/2
      1/28	1/4

      So the answer is 1/2+1/4+1/14+1/28 (we usually order them from largest to smallest).

      Notice that the Egyptians didn't use decimals -- you shouldn't either! They also didn't combine fractions, or use mixed numbers (so they wrote "3 + 1/2" rather than "3 1/2").

      Why did Egyptians do things this way? (an example division problem, 3/5).

         Dominic Olivastro, "Ancient Puzzles", suggests a third reason why 
      this use of unary fractions is good. Consider the problem Ahmes poses 
      of dividing 3 loaves of bread between 5 people. We would answer "each
      person gets 3/5-ths of a loaf". If we implemented our solution, we might
      then cut 2 loaves into 3/5 | 2/5 pieces, with bread for 3 people; then
      cut one of the smaller pieces in half, giving the other two people 
      2/5 + 1/5 pieces. Mathematically acceptable, but try this with kids and
      they will insist that it is not an even division. Some have larger pieces,
      some have smaller.
      

      Samm said it's called "sibling math" (and this family Circus comic shows why!).

      Ahmes would calculate 3/5 as :
         3/5 = ()3 + ()5 + ()15    [ = 1/3 + 1/5 + 1/15 ]
      Now cut one loaf into fifths, cut two more into thirds, then take one of
      the 1/3-rd pieces and cut it into 5-ths (for the 1/15-th pieces), and you
      can now distribute everyone's 3/5-ths share in a way that _looks_ equal,
      since they will have exactly the same size pieces. (And no, I don't want
      to argue about the crust.)
      

    • There is another way to get these answers, using the Fraudini trick and the Unit Fraction Table. So let's try those same examples but using the unit fraction table rather than our doubling tables.
      1. $\displaystyle \frac{35}{8}=\frac{32+2+1}{8}=4+\frac{1}{4}+\frac{1}{8}$

      2. $\displaystyle \frac{6}{7}=\frac{4+2}{7}=\frac{4}{7}+\frac{2}{7} =2\frac{2}{7}+\frac{2}{7} $

         so we look up $\frac{2}{7}$ in the unit fraction table, and find that $\frac{2}{7}=\frac{1}{4}+\frac{1}{28}$. Therefore,

         \[ \displaystyle \frac{6}{7}= 2*(\frac{1}{4}+\frac{1}{28})+\frac{1}{4}+\frac{1}{28}= \frac{1}{2}+\frac{1}{14}+\frac{1}{4}+\frac{1}{28} \]

      which is exactly what we got before -- except they're not in order from largest to smallest.

      

    • Here's a relatively easy one: Suppose Fatima had 3 loaves to share between 4 people. How would she do it? (Think about what the answer means, in terms of bread, and keeping kids happy.)

    • A little trickier:
      1. How would you divide 5 by 7?

         (Start with halves, and then what?)

      2. How can we use the unit fraction table to get the same answer?

    • How would you like to do story problems like this one?!

We're going to do three things today: solve two mysteries, and celebrate our hero Zero.

• How do you like this t-shirt?
  

  You should be ready to get the joke. And I'm hoping that, by the end of the day, you'll have come up with some more joke shirts!

• We begin by playing Sherlock Holmes in Babylon

  The author, Prof. Buck, guesses that "the document" (actually a clay tablet) comes from the city of Nippur, in what is now Iraq:

  

  Buck says this "Confronted with an artifact from an ancient culture, one asks several questions:

  1. What is this and what are its properties?
  2. What was its original purpose?
  3. What does this tell me about the culture that produced it?
  So: this is a representation of a clay tablet, with markings in it.

  Your job: to describe the markings, and investigate the patterns on this tablet.

  • What can we deduce about
    • the purpose of the table?
    • the way (and reason) Babylonians wrote their numbers the way they did?
    • the Babylonians and place value?
    • the Babylonian's missing number(s)?
    • the Babylonian influence in our world today?

  • How would the Babylonians write these numbers:
    1. 47
    2. 573
    3. 1,60, and 3600

  • What do you think of this t-shirt?

  ---

• The frequently unsung hero of the Hindu-Arabic numbers is the digit 0 -- a symbol for nothing! (The Babylonians can't distinguish the numbers 1 from 60, without some additional context -- they had no hero).

  Well let it be unsung no more! I hope that you'll enjoy this rendition of

  Zero, My Hero

  (favorite lyrics: "et cetera, et cetera; ad infinitum; ad astra¹; forever and ever")

  ---

• Now to the mystery of the Mayans.... Same questions:
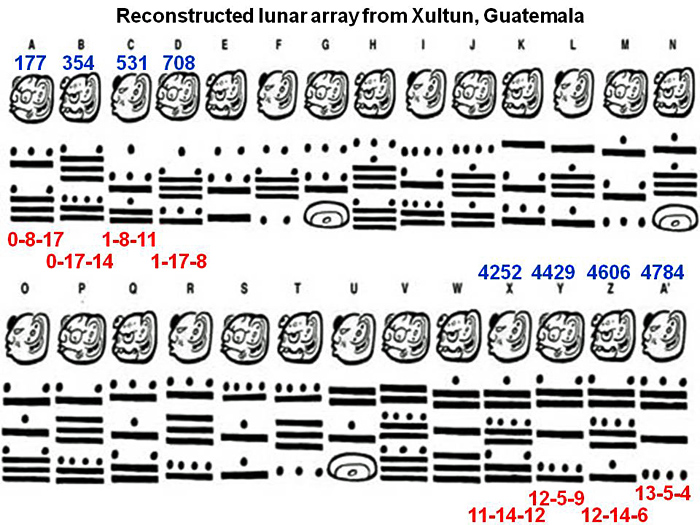
  • What can we deduce about
    • the Mayans and place value?
    • the purpose of the table?
    • the way Mayans looked at numbers and their world?
    • the Mayan influence in our world today?

  • How would the Mayans write these numbers:
    1. 47
    2. 573
    3. 3600
    4. 14001

• Do math like an Egyptian! (Walk Like An Egyptian/Michael Jackson Mash-up!)
• Hexagonal Paper
• Pascal's triangle (wikipedia)
• American Bandstand dances to Gimme Some Lovin', a hit by The Spencer Davis Group: here's their version.
• List of musical works in unusual time signatures
• Blue Rondo a la Turk, by Dave Brubeck: illustrating how to play a piece in 9/8.

  Watch Dave Brubeck's leg, counting out the rhythm....