- Your quiz today will feature Egyptian Mathematics, and using Pascal's triangle to count things or to compute probabilities.
- Next week we finish up this "number unit" with the third great factorization; then, the week following, we'll have our first exam (on Thursday, 2/27). Start studying up! Make sure that you do your readings, as they will be a part of the exam.
- We tried more examples of Egyptian division, and noted that the
representation of a fraction might not be unique.
We did some of the divisions in a way analogous to the multiplication table; we also used the "Unit Fraction Table" to find the same answers, relying in part on the "Fraudini trick".
- We then continued to discuss Babylonian mathematics, in particular
the object (clay tablet) which turned out to be a nine times
table.
We discovered that the Babylonians had a positional number system with a base of 60, but no Zero, My Hero. That means that they had only 59 digits, and here they are:

Add one to fifty-nine, and you get sixty: and so we bump up a place, and put another one in there.
A base sixty system is "sexigesimal".
As a review, how do we write
- 10,000 as a Babylonian number?
- How about 216,000?
Did you ever notice how we block numbers into threes?:)
- Based on this artifact, the Xultun (shool-TOON) lunar calendar:
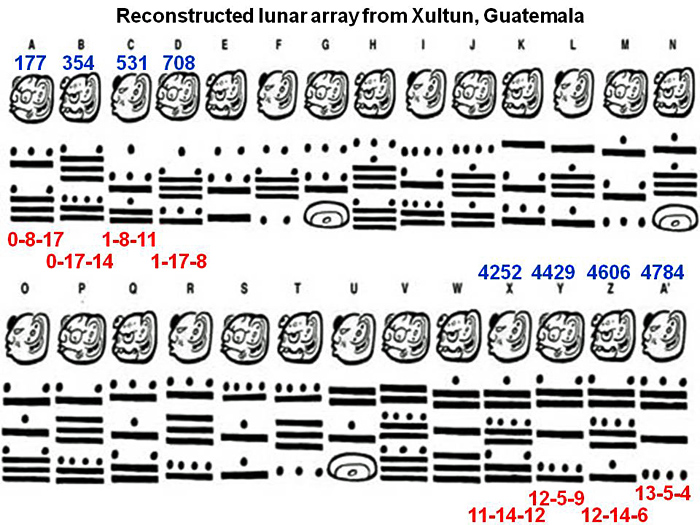
- What can we deduce about
- The Mayans and place value?
- The purpose of the table?
- The way Mayans looked at numbers and their world?
- The Mayan influence in our world today?
- Sean noticed that the first four numbers at the top were just multiples of 177. But that eventually fails. In which column?
- If you recall from Zero, My Hero, there are
people who "counted on their fingers and toes...."
A base 20 system is called "vigesimal". The Mayans had
a quirk in their system, however, which rendered it an
impure base-20 system (you'll know this, if you did
your reading!). It's a "mostly vigesimal" system. But
the third place should have been \(20^2\): what is it?
(Column c can tell us....)
After that, however, the Mayans used multiples of 20 to
increase the numbers in the next positions: 1, 20, 360, 360*20=7200, 360*202=144000, etc.
- How would the Mayans write these numbers:
- 47
- 400
- 573
- 3600
- 7200
- 14001
- "All that remains now is for us to discuss the reasoning
behind the 177- and 178-day intervals of the reconstructed
Xultun lunar table (Figure 11).
It has long been known that pages 51-58 of the Dresden Codex contain a lengthy lunar table, sometimes called the Dresden Codex eclipse table (Figure 12). The Dresden Codex calculates moons in intervals of six lunations (177 days), with an occasional correction of five lunations (148 days) over a period spanning 11,958 days, or 405 total lunations (see Aveni 2001:173-184 for a thorough discussion). This works out to an average of 29.52593 days per lunation [ael: about 42517 minutes]. Mayanists have long marveled at the accuracy of this table, which places the average length of a lunation within seven minutes of the modern figure of ~29.53059 (Aveni 2001:183). More fascinating still, however, is that the recently discovered Xultun table actually comes even closer to the modern value. It will be remembered that the Xultun table covers a total of 4,784 days and represents 162 lunations (Saturno et al. 2012:715), which works out to a mean length of 29.53086 days per lunation, or within four minutes of the modern figure."
(from Unearthing the Heavens: Classic Maya Murals and Astronomical Tables at Xultun, Guatemala)
The Mayans were very good at counting!
- What can we deduce about
- Time for a quiz....
- A review of the Mayan calendar we study, Unearthing the Heavens: Classic Maya Murals and Astronomical Tables at Xultun, Guatemala , including the reference to this article from the journal Science: Ancient Maya Astronomical Tables from Xultun, Guatemala, and this more "popular" interpretation of the calendar.
- Do math like an Egyptian! (Walk Like An Egyptian/Michael Jackson Mash-up!)
- Hexagonal Paper
- Pascal's triangle (wikipedia)
- American Bandstand dances to Gimme Some Lovin', a hit by The Spencer Davis Group: here's their version.
- List of musical works in unusual time signatures
- Blue Rondo a
la Turk, by Dave Brubeck: illustrating
how to play a piece in 9/8.
Watch Dave Brubeck's leg, counting out the rhythm....