- This week's quiz will be over gold, and spirals.
- Assignment to turn in: Use the Fibonacci
Spiral Fractal maker, with your own image, to make a photo Fibonacci spiral.
You might try some of the "art" features.
Email me this, and we'll hold an art show of spirals, with "get out of quiz free" prizes....
(Due Wednesday, 3/5)
I already have some entries!
- You also have a fairly lengthy homework assignment, so please get started on it.
- We had an exam: let's talk about it:
- Median score: 76 (top score: 97)
- Key
- A couple of comments:
- Make sure that I added up your points
correctly: the amount that you earned
on a page should be in the bottom left
corner.
- Feel free to argue if you feel that I
didn't give you points you
deserved. Sometimes I miss "your
point", and if you can make a case for
yourself, do so!
- I scored a whole bunch of points at Nim :(
- Are there any in particular that you want to talk about?
- Make sure that I added up your points
correctly: the amount that you earned
on a page should be in the bottom left
corner.
The Golden rectangle is much like Fibonacci's -- only better! It's the limiting case of what Fibonacci's would look like if you could go on forever with your Fibonacci spiral.
We'll encounter the golden mean again in the context of our study of Platonic solids, and I'll make mention of the golden rectangle in the context of symmetry.
- We're starting a new topic, one which I think is
beautiful (and I hope that you'll agree). Let's talk about
symmetry:
Symmetry, as wide or as narrow as you define its meaning, is one idea by which man through the ages has tried to comprehend and create order, beauty and perfection. Hermann Weyl (German Mathematician; 1885 - 1955) - Where have we seen (or used) symmetry already?
- Yanghui's triangle had an error in it, that we found by assuming symmetry.
- We used symmetry when drawing complete graphs: "Start with
a regular polygon..." I might have said.
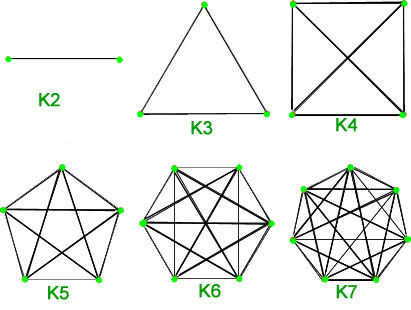
I'm terribly fond of this graphic I made to illustrate all distinctly different simple graphs with five vertices: my goal was to use symmetry to advantage.

- There's a beautiful symmetry in Pascal's triangle, and in
its mathematical usefulness:

The problem of choosing 3 friends from 5 to go to the show
is symmetric to the problem of choosing 2 (= 5-3) friends from 5 to not go to the show.
- There's a type of symmetry in the Fibonacci (or golden)
rectangle: within a golden rectangle is found a perfect
scale copy of itself.
We might call this "symmetry of scale" -- two identical copies of a thing, but of different sizes:
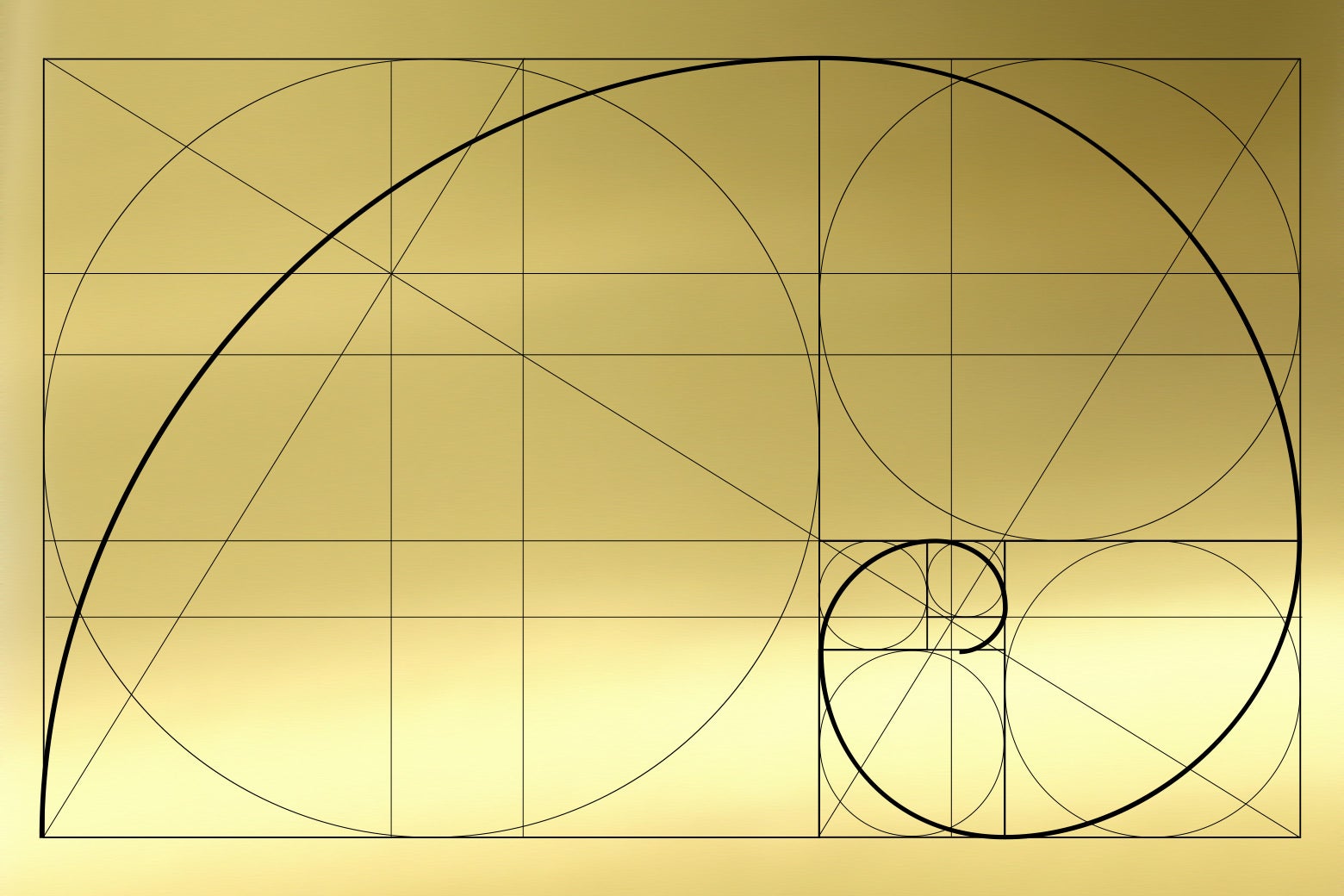
Where else does symmetry appear, and how do we use it?
- Here's a video clip of Fred Astaire and
Ginger Rogers.
- You'll notice many times when Fred and Ginger are
"mirroring" each other; this is sometimes referred to
as a "mirror reflection" (or "reflection symmetry"):
one type of symmetry.
-
But in this clip you'll also see symmetry of scale, and
what we might call "translational symmetry": a copy
displaced from itself.
-
And notice that it is funny, or jolting, when symmetry
is broken:




Just like it was "jolting" when Yanghui's triangle failed symmetry in the 35 position....
By the way: they say Fred Astaire was pretty good (well, "the best dancer ever"); but Ginger Rogers did everything Fred did, only backwards (and in heels...).
- You'll notice many times when Fred and Ginger are
"mirroring" each other; this is sometimes referred to
as a "mirror reflection" (or "reflection symmetry"):
one type of symmetry.
- Today in the New York Times, they introduced a new feature:
You stare at a photo for 10 minutes.
I only made a minute, but I'm glad that I checked out the description afterwards: they describe how the reflective symmetry played a role in making this an image worth focusing on for ten minutes!:)
- Along the same lines is this clip of
Lucille Ball and Groucho Marx:
I Love Lucy!
- Are
humans symmetric? Turns out that we're purported to have a "good
side" and an "evil side"!
Years ago a couple of my students tried the facial symmetry trick. It came back, on TikTok.
Humans possess bilateral symmetry: we have mirrored sides. At least to external appearances. Inside, of course, some of our organs are on one side or the other. That's an interesting twist!
"Our sensory organs and central nervous system are, as the result of evolutionary development, genetically programmed to recognize regularity, and hence order."
"Patterns" are, in some sense, a symmetry: that the same thing is repeated. It leads to predictability.
- Which "face" did
babies focus on?
Remember how I say that mathematicians are pattern seekers? Newborn babies are already seeking patterns....
- Composite
versus designed faces
- "In experiments, test subjects found computer-generated composite (averaged) images of faces more attractive than the many individual faces, from which the composite images were generated." (p. 23)
- "[test subjects] developed a face which strongly resembled the average face of the population in which they lived, but which was characterized by more child-like features."
- Which "face" did
babies focus on?
- Here are some other of Earth's creatures -- which ones also have
bilateral symmetry? What other kinds of symmetry do you see?
Symmetry
of life forms on Earth
A phenomenal scientist and artist, Ernst Haeckel, discovered and documented many of the radiolaria. Let's check out a little of a video featuring many of his fantastic images: On the Discovery Docket: Proteus (local copy)
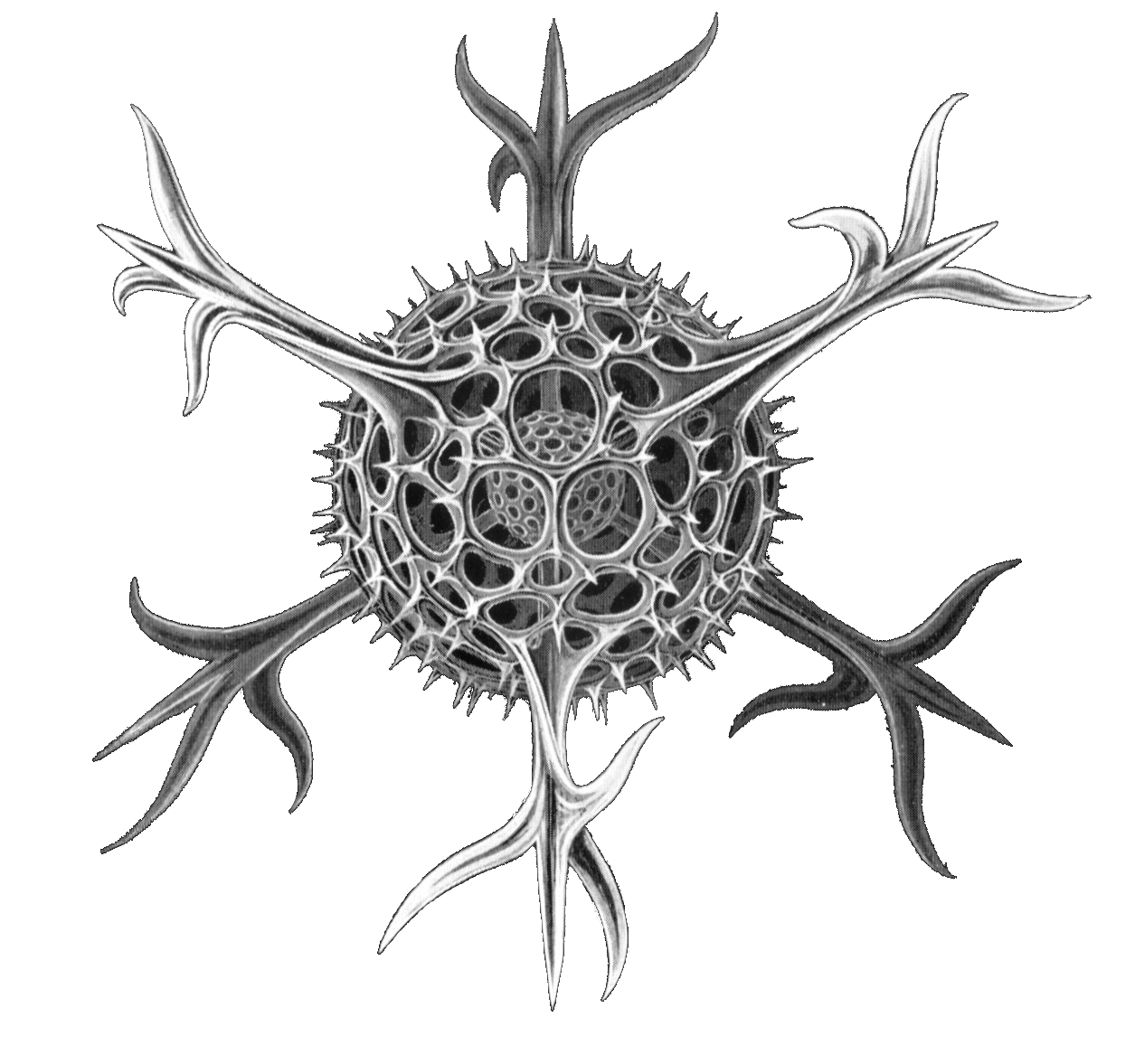
"They are like an alphabet of possibilities, as if the ancient sea were dreaming in its depths all the future permutations of organic and invented form. From backbones to bridges, and from the earth to the stars."
- Symmetry can be used by us humans in two different ways:
- to simplify, and
- to complexify.
- Making things simpler (too simple?): graphic designers
"fake" the true recycling symbol with one arrow, which they
copy and rotate to make their "faux recycling symbol" (the true
one is on the right, and you'll see that the arrows are not all
the same).


- Complexifying: Making things more interesting!
These dances (and others, like square dances) effectively illustrate rotational, mirror, and translational symmetries.
- Now to help us break down some of the most important elements of
these topics, I want to distribute this
worthy handout, or four pages of it at any rate.
It covers two kinds of symmetry that are very important: rotational and reflective.
So let's take a look! Your homework is to complete it.
- In the plane of 2-Dimensions,
- What is the most symmetric rectangle?
- How would you define the regular polygons:
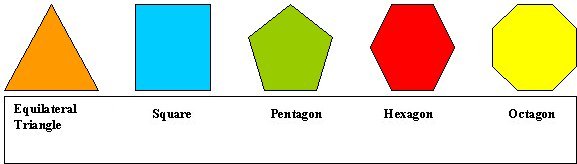
- How many regular polygons are there?
- What kinds of symmetry do they possess?
- Which regular polygons can be used exclusively to "tile" the plane, like a bathroom floor?
- Using symmetry in a process, to build complete graphs. Let's try \(K_6\)!
- Where have we seen (or used) symmetry already?
- Meet the world's Mrs Averages: Scientists blend thousands of faces together to reveal what the typical woman's face looks like in 41 different countries from around the globe
- Comparing
theory--driven and data-driven attractiveness models using images of
real women's faces
This paper contains a lot of references, and on-line resources to document their work.
- The Brain's
Face Recognition System Is Easy to Fool:
The human brain is good at identifying faces, but illusions can fool our "face sense"
"Because the human brain is so good at detecting faces, we sometimes see them where they do not exist. Were you ever scared as a child by strange faces popping up from an abstract wallpaper design or formed by shadows in the semidarkness of your bedroom? Ever notice that cars seem to have faces, with the headlights as eyes and the grilles as mouths? These effects result from the face-recognition circuits of our brains, which are constantly trying to find a face in the crowd."
- Modeling individual preferences reveals that face beauty is not universally perceived across cultures
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Hexagonal Paper