Function Composition

There are many ways to create new functions from old. We can add two functions together, such as

${x+\sqrt{1+x^2}}$

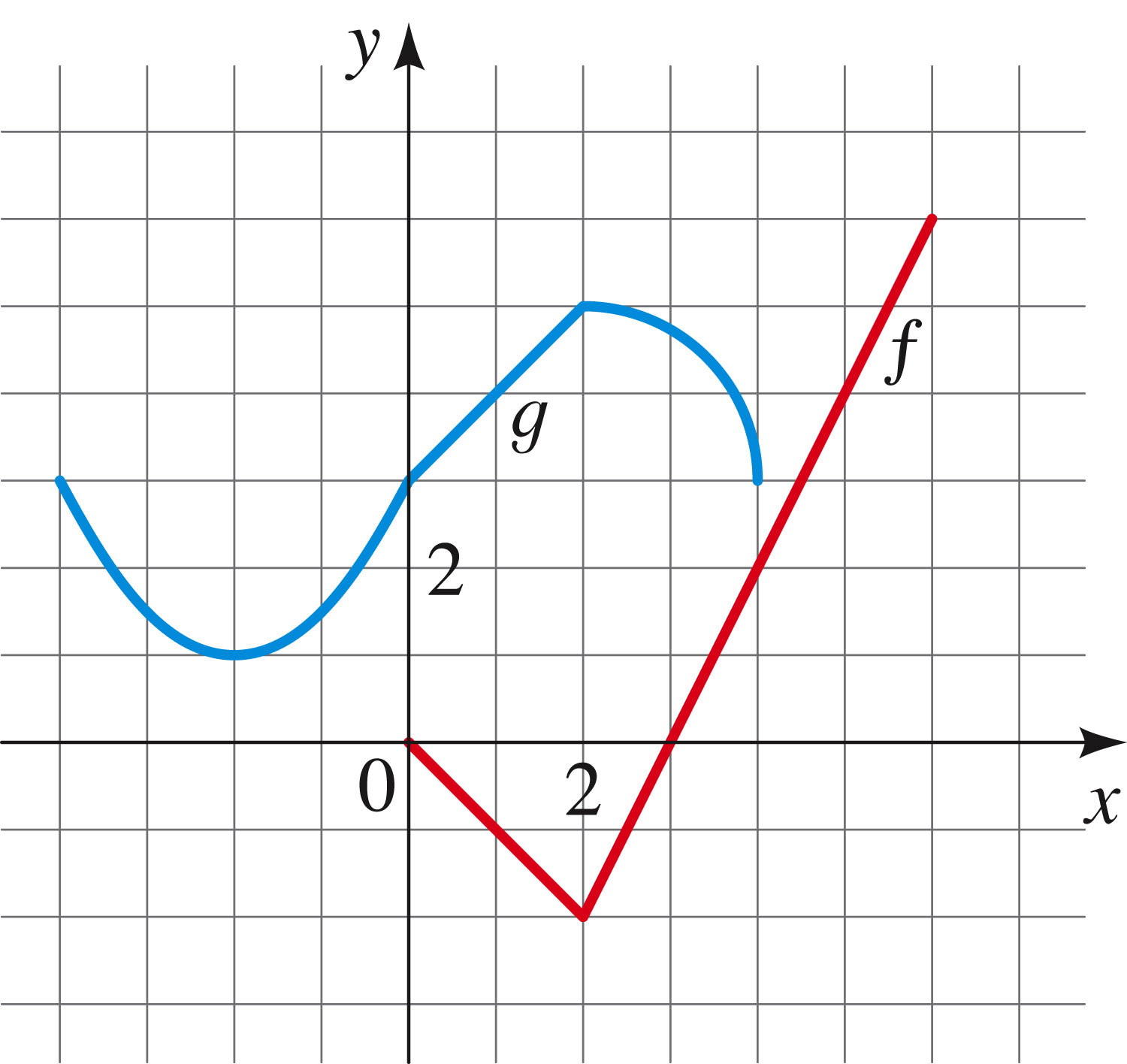
We can also subtract them, multiply them, and divide them. So the usual algebraic manipulations allow us to create new functions from old.

A somewhat more complicated operation is that of function composition, in which two (or more) functions are applied sequentially. An example is the function

${\sqrt{1+{x^2}}}$

from above. First the polynomial function ${1+{x^2}}$ operates on x, and the square root function then operates on the result. Pictorially we might write this as

\[ x {\rightarrow} 1+x^2 {\rightarrow} \sqrt{1+{x^2}} \]

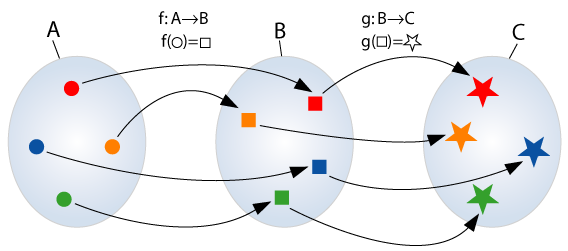
Note: we could consider this as a composition of even more functions:

${x {\rightarrow} x^2 {\rightarrow} 1+x^2 {\rightarrow} \sqrt{1+{x^2}}}$

Now, what did each function -- represented by the long arrows -- do? Each transforms whatever it receives (starting from x) into something that it hands along to the next function:

The first function squared x (let's call the result y);
The second function added one to the resulting y (let's call that z);
The third function takes the square root of z, and represents the final result (call it w).

If we give each function a name, then we might write the three this way:

${f(x)=y=x^2}$
${g(y)=z=1+y=1+x^2}$
$h(z)=w=\sqrt{z}=\sqrt{1+y}=\sqrt{1+x^2}$

Notice how we use different names for the independent and dependent variables. This is like using the different symbols used in the image above (circle, square, star).

Then the function

${\sqrt{1+x^2}=h(z)=h(g(y))=h(g{(f(x))})}$

${\sqrt{1+x^2}=h(g(f(x)))}$

In fact, the transformations we've already considered are examples of compositions:

Vertical shift up by c:	${x} \rightarrow {f({x})} \rightarrow {f({x})}+c$
Horizontal shift right by c:	${x} \rightarrow {x-c} \rightarrow f({x-c})$
Reflection over the x-axis:	$x \rightarrow f(x) \rightarrow {-f({x})}$
Reflection over the y-axis:	$x \rightarrow -x \rightarrow f(-x)$
Vertical stretch by a factor $a$:	$x \rightarrow f(x) \rightarrow {a*f(x)}$
Horizontal stretch by a factor $a$:	$x \rightarrow ax \rightarrow {f(ax)}$

Some exercises to try: pp. 196-, #5, 15, 21, 35, 41, 45, 49, 63

For exercises #27-32:

Website maintained by Andy Long. Comments appreciated.