Invertible Functions

An invertible function
The SSN you have is yours alone: no other (living) person has your SSN.
So we can consider the function SSA that associates Americans with their unique SSNs. Now the Social Security Administration (SSA) can take your name and give your SSN; furthermore, if I give them a SSN, they can tell me your name. That is, they can go back and forth between their domain and range. They can go "backwards".
So really we can think of two functions here: one, call it ${SSA}$ , that has as its domain names, and returns SSN numbers (which are in the range); from that function, we can define another function, call it ${SSA^{-1}}$ , which has its domain SSN numbers, and which returns names in its range.
A non-invertible function
Now here's a function that won't work backwards. Consider the function IRS, which takes your name and associates it with the income taxes you paid last year. While the IRS can take your name (and SSN!), and tell how much you paid in taxes (let's say that it was $500), they can't take a dollar amount ($500) and tell your name -- because there might be 100,000 people who paid that amount in taxes. The tax amount is not unique to you, in general.
a one-to-one function
The first kind of function is called a one-to-one function, and it is invertible -- that is, from it we can create another function which goes backwards, from the range of the original function to the domain. Here's a picture of the situation:

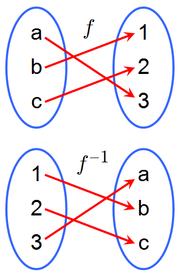
Notice the notation: the inverse of ${f}$ is ${f^{-1}}$ , and the domains and ranges of the two are interchanged.
A graphical test for one-to-one-ness (that is, invertibility)
Graphically, we use the horizontal line test to see if a function is one-to-one:

Left: one-to-one
No horizontal line crosses more than once
Right: not one-to-one
Here's a horizontal line that crosses more than once

If no horizontal line crosses the function more than once, then the function is one-to-one.

one-to-one ${\Leftrightarrow}$ no horizontal line intersects the graph more than once
Question: which functions in our function zoo are one-to-one, and hence invertible?
Inverse function property:
1. ${f^{-1}(f(x))=x}$ :
  This says ${f}$ maps ${x}$ to ${y=f(x)}$ , then ${f^{-1}(f(x))}$ sends ${y}$ back to ${x}$ .
2. ${f(f^{-1}(y))=y}$ :
  This says ${f^{-1}}$ maps ${y}$ to ${x=f^{-1}(y)}$ , then ${f(f^{-1}(y))}$ sends ${x}$ back to ${y}$ .
Here's an example. You might know that the square function and the square root function are inverses. That is, if , then . So take an example value of . Then

${f(2)=4}$ and ${f^{-1}(4)=2}$
The role of ${x}$ is played by 2; the role of ${y}$ is played by 4.
How to find the inverse of a one-to-one function:
1. Write ${y=f(x)}$ .
2. Solve this equation for x in terms of y (if possible)
3. Interchange x and y. The resulting equation is ${y=f^{-1}(x)}$ .
  This is the silly step! Because our favorite independent variable is x, we do this. There's no reason not to leave the inverse as
  ${f^{-1}(y)=x}$
  It will just bother most textbook writers.
  In fact, it's better to leave it this way, because it indicates that the domain of ${f}$ is the range of ${f^{-1}}$ (and vice versa).
  If you understand why I'm making a big deal about this, then you're doing really well. Keep it up! If you don't understand, ask a question.
Graphing the Inverse of a Function:
It's easy, if you have the graph of ${f}$ : just reflect the graph of ${f}$ across the line ${y=x}$ :

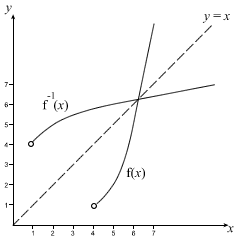
Why does this work? Because the inverse function ${f^{-1}}$ just swaps the domain and range of ${f}$ , which means that the x and y-axes are swapped.
We've already seen examples of invertible functions:
Notice that the example of function composition has invertible functions everywhere:

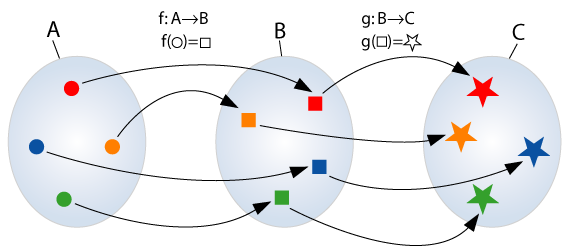
From this picture we can conclude that the composition of invertible functions is invertible on its domain.