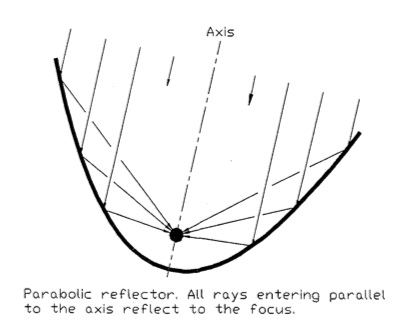
- Parabolas are extraordinarily important. Nature loves them:
Can you think of any others?
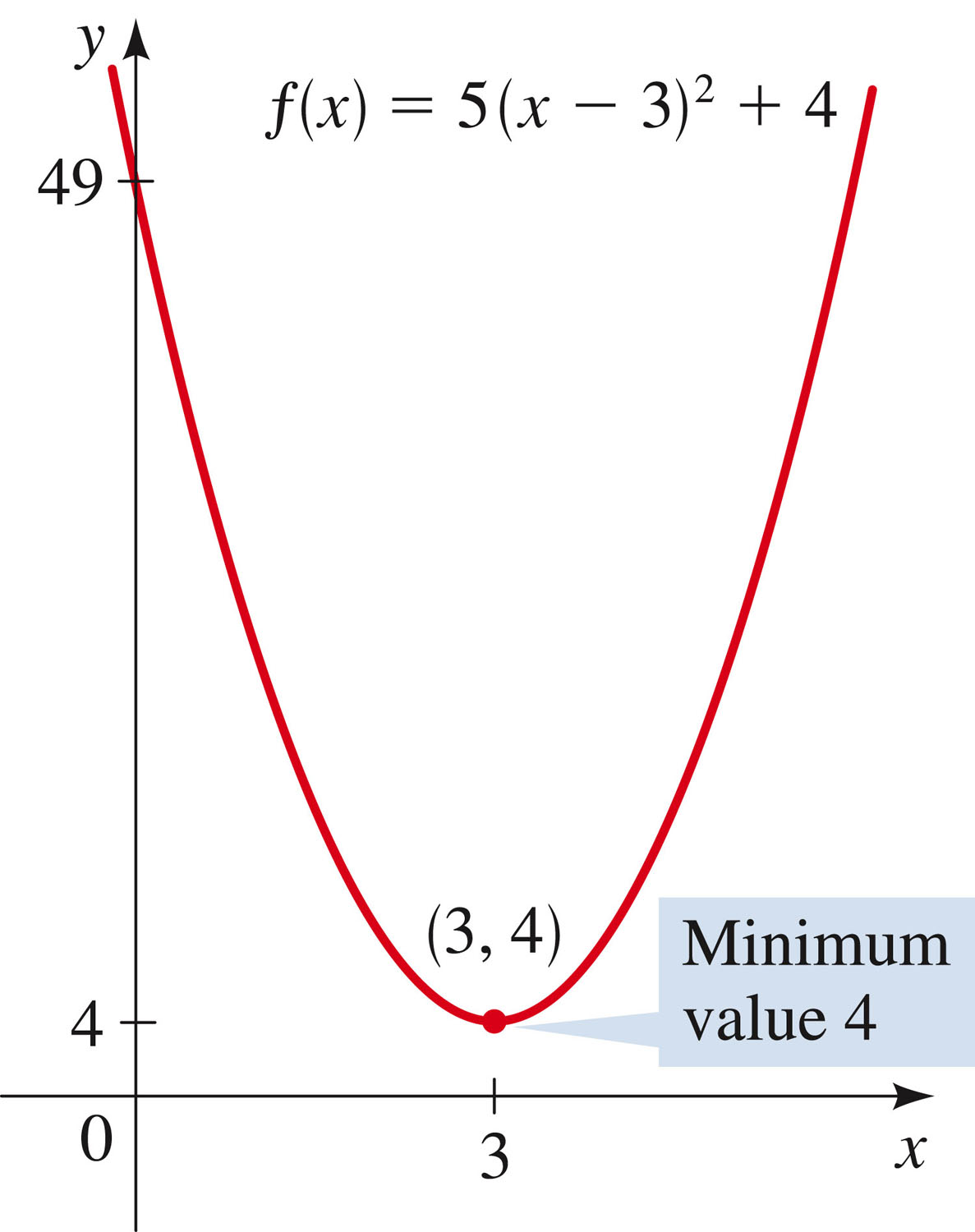
- These are the graphs of quadratic functions, which are second-degree polynomials:
=ax^2+bx+c})
- Now, there are two kinds of parabolas: bowls and umbrellas.
If  , we've got a bowl;
, we've got a bowl;
if  , we've got an umbrella:
, we've got an umbrella:
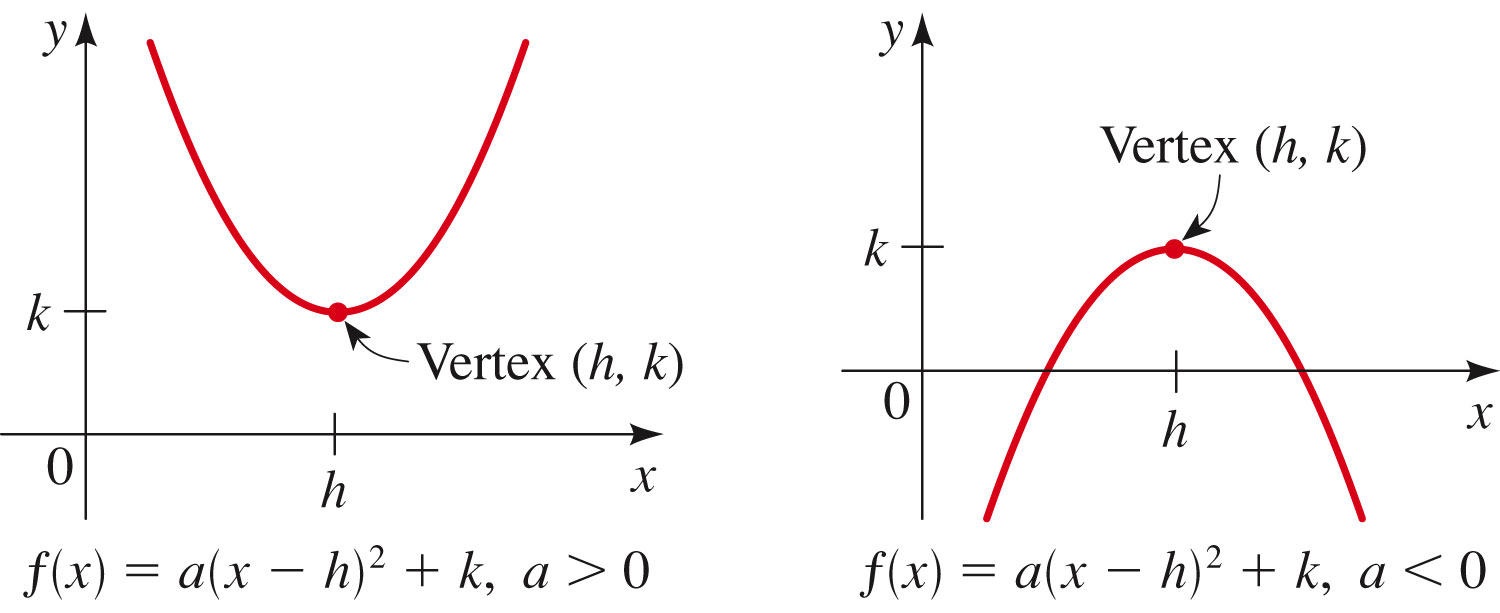
Can you see how to build up any parabola from  as a stretch, horizontal shift, and vertical shift?
as a stretch, horizontal shift, and vertical shift?
- Look at the form of $f(x)$ in
that image above: those two forms are called the standard form
of the quadratic. Every quadratic can be expressed in standard form (using a technique called "completing the square").
- Finally, every quadratic $f(x)$ can be expressed in the form $a(x-r_1)(x-r_2)$ where $r_1$ and $r_2$ are the roots given by the quadratic formula.
Exercise #13, p. 230
- Let's take a look at that in Mathematica
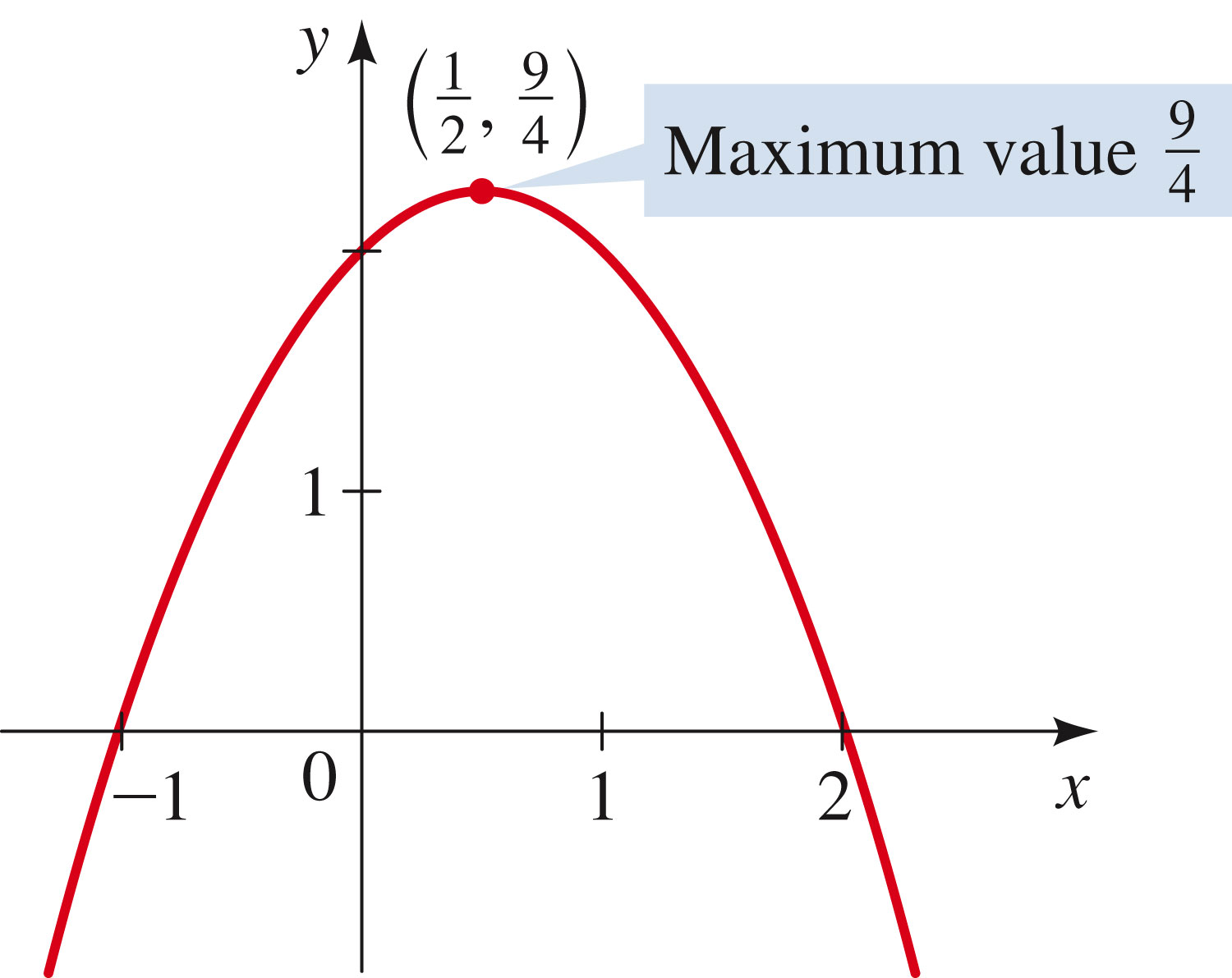
- Now one of the things that quadratics do that linear functions cannot is
hit a maximum and turn around (or hit a minimum and turn around).
(Linear functions are polynomials of first degree, whose graphs are
straight lines.)
Exercises #25, 27, 33, and 35, p. 230
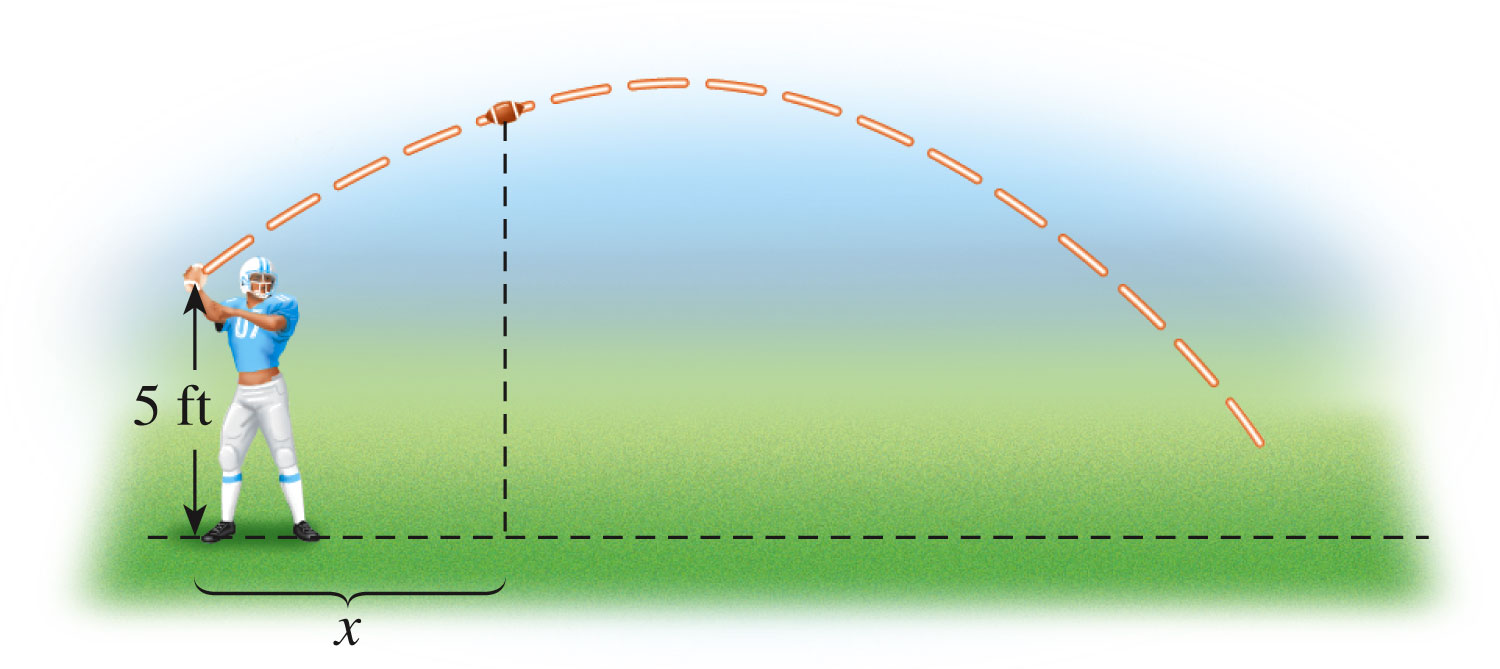
- Now: modeling. Let's look at a couple of applications of quadratic functions:
Exercises #67, p. 231 and #77, p. 232.
, we've got a bowl;
, we've got an umbrella:
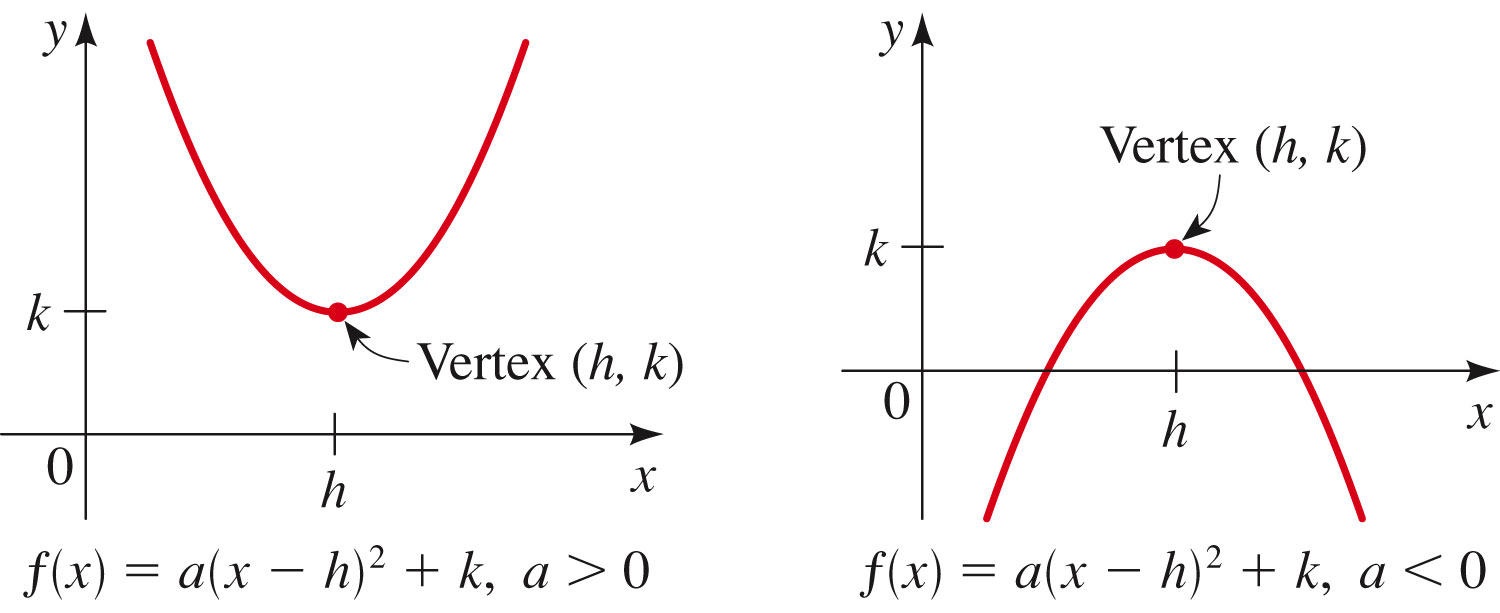
as a stretch, horizontal shift, and vertical shift?