- Rational Functions and Asymptotes
- Transformations of
- Asymptotes of Rational Functions
- Graphing Rational Functions
- Slant Asymptotes and End Behavior
- Applications
A rational function is a ratio of polynomials:
What can go wrong? We've got a denominator: perhaps it's zero, which would be bad....

This function is interesting: it is odd (possesses symmetry), it is its own inverse, and its graph is made up of special functions called hyperbolas:

- Consider rational functions of the form
Each one of their graphs can be obtained from that of 1/x by transformations. Let's see how -- by long-division.
- Mathematica Demonstration of these linear fractional transformations
Here's two of the most important things about rational functions:
- They have vertical asymptotes (where the denominator polynomial is zero but the numerator polynomial is not zero), and
- They have end-behavior asymptotes (when x gets big in size, tending towards
)

The end-behavior asymptote is the polynomial that the function approaches as
.
This might be a horizontal asymptote (which means that , a constant function):

This might be a slant asymptote (which means that , a linear function):

Or this may be more complicated (e.g. a quadratic asymptote, where , a quadratic function):
It turns out that every rational function can be expressed as the sum of a polynomial and rational function
where the numerator degree is less than the denominator degree:
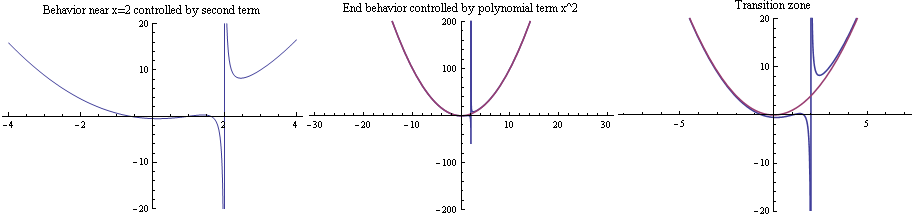 |
||
|
|
||
| The inner behaviour (near zero) | The end behavior (as |
The transition zone, where both terms are clearly visible |
|
|
||
The way we find the end-behavior asymptote is via long-division (I hear you groan!). Let's try one....
The graphing strategy for rational functions is the same as for polynomials, only we include the asymptotes.
- Mathematica Demonstration of rational functions