Inverse Trig Functions

There are two primary trig functions:
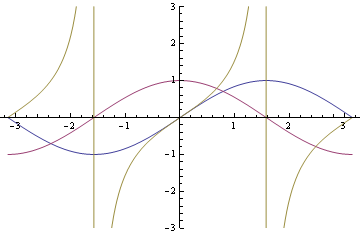
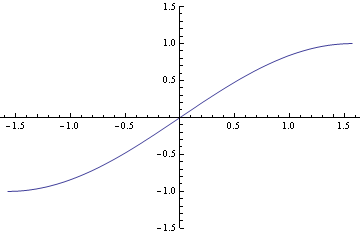
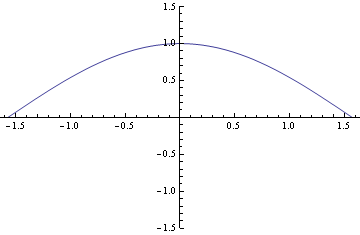
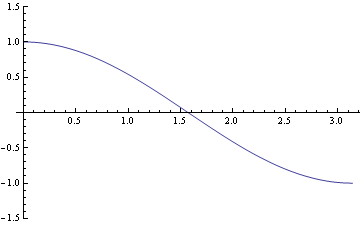
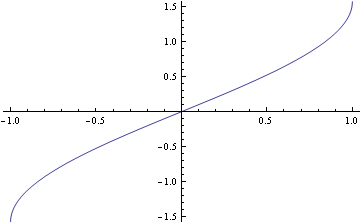
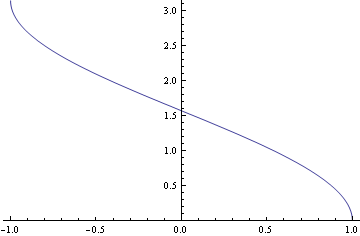
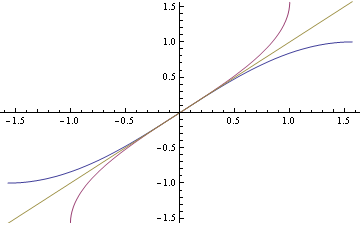- sine and cosine (which is which? -- remember that sine is odd, and cosine is even):
  
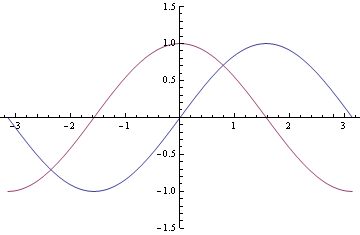
  We discovered last time that it is only necessary to graph these on one "period" -- once "cycle" of ${2\pi}$ -- because after that they repeat. If you make any extra full trips around the circle (either clockwise or counterclockwise), the points are coterminal, and so the ${(x,y)}$ pair is unchanged, so the sine and cosine are unchanged.
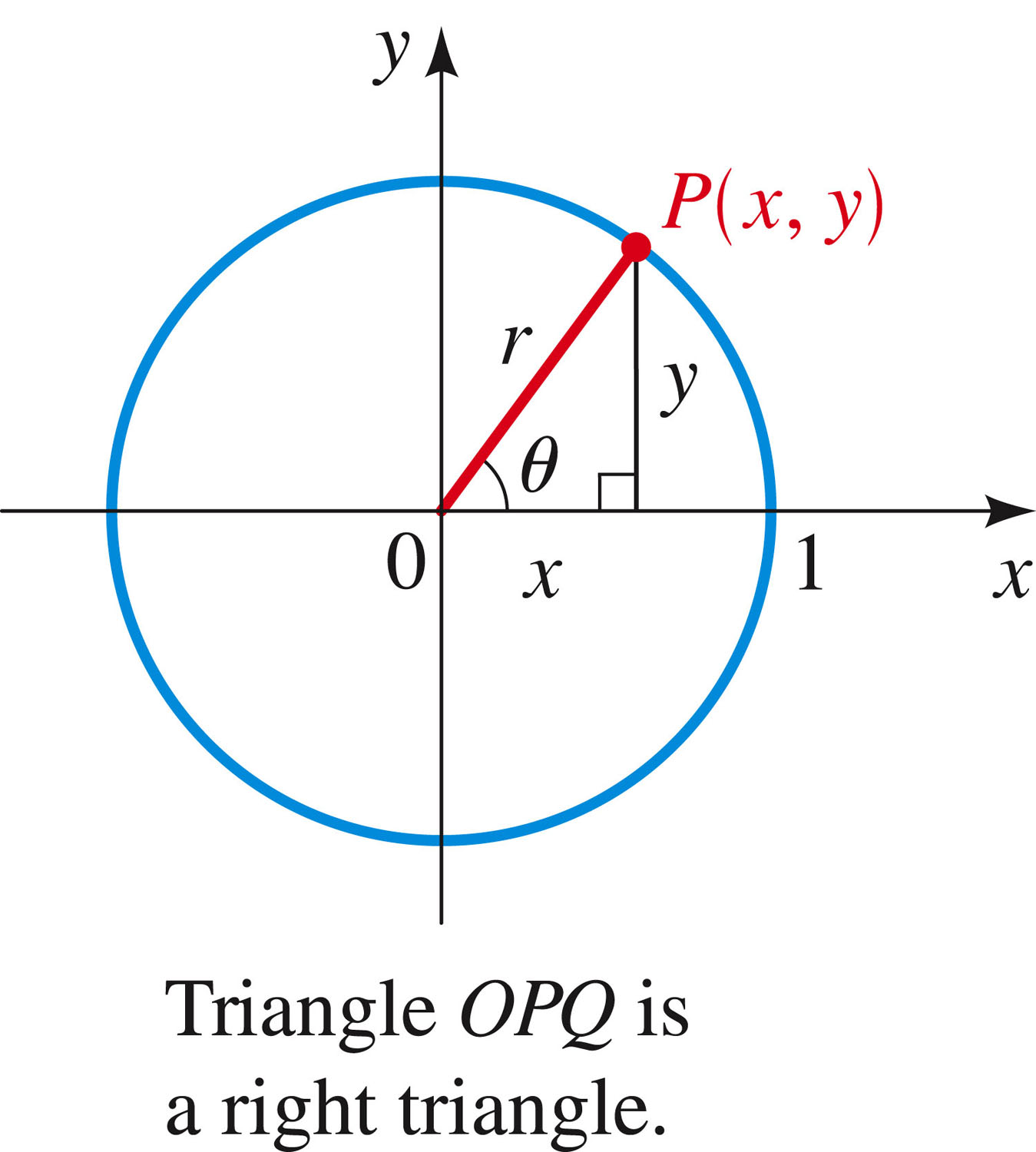
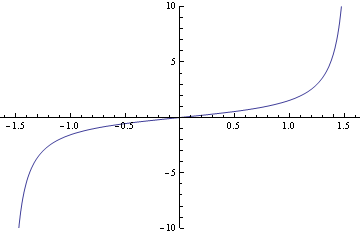
- from which we derive a third (tangent -- notice that it has vertical asymptotes when cosine is 0, and repeats more frequently than sine and cosine. We say that the period of tangent is ${\pi}$ , whereas the periods of sine and cosine are ${2\pi}$ ):
  
  ${\tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}}$

Q: do any of these three functions pass the horizontal line test?

Inverses of Trig Functions

In order to define inverse functions, we will need to restrict the domains of the trig functions. Tangent is one-to-one (remember that?) on its period of ${\pi}$ , so we can restrict our attention to ${\left(-\frac{\pi}{2},\frac{\pi}{2}\right)}$ . On that same interval, we see that sine is also one-to-one:

Cosine is not one-to-one on this interval

However, if we simply shift the interval to ${\left(0,{\pi}\right)}$ , we get a one-to-one version of cosine:

So here are pictures of arcsine, arccosine, and both sine and arcsine together (showing that the graphs are obtained by reflecting about the line y=x:

Consequences of restricting the domains

Just like for the square root function, we have a slight problem because we've restricted the domains. For the square root function, we have

${(-2)^2=4}$ but ${2=\sqrt{4}}$
In some sense, we can't recover the -2 using the "inverse" of ${x^2}$ (because the restriction of the domain eliminated all the negatives).
The same problem happens for the sine function, for example:

${\sin(\frac{3\pi}{4})=\frac{1}{\sqrt{2}}}$ but ${\arcsin(\frac{1}{\sqrt{2}})=\frac{\pi}{4}}$
We can't recover the ${\frac{3\pi}{4}}$ .

Now let's do some problems.

#5, p. 467
#15 and 17, p. 467
#28, p. 468
#37, p. 468

Website maintained by Andy Long. Comments appreciated.