
As the author mentions, this question is central to the art and science of surveying. There's a great historical note about surveying the Himalayas -- I hope that you notice such things in your textbook.
The short answer:
(And provided that the triangle actually exists!)
The four distinct cases we need to consider are

The case of AAA cannot be solved, because we don't know the scale. We could double the length of all sides without changing any of the angles, so clearly AAA is not uniquely solvable.
The law of sines establishes a relationship between sines of angles and the lengths of their opposing sides:
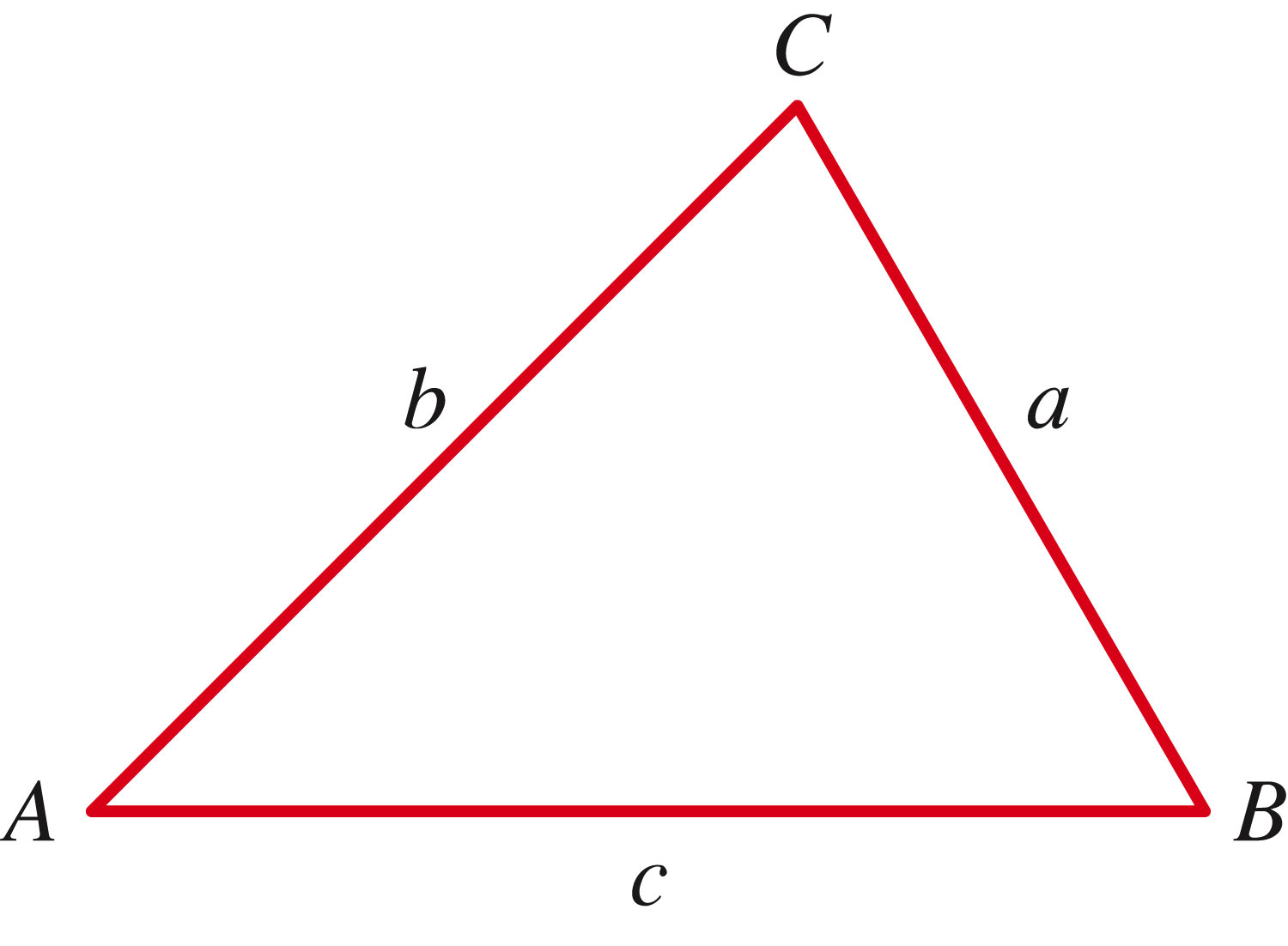
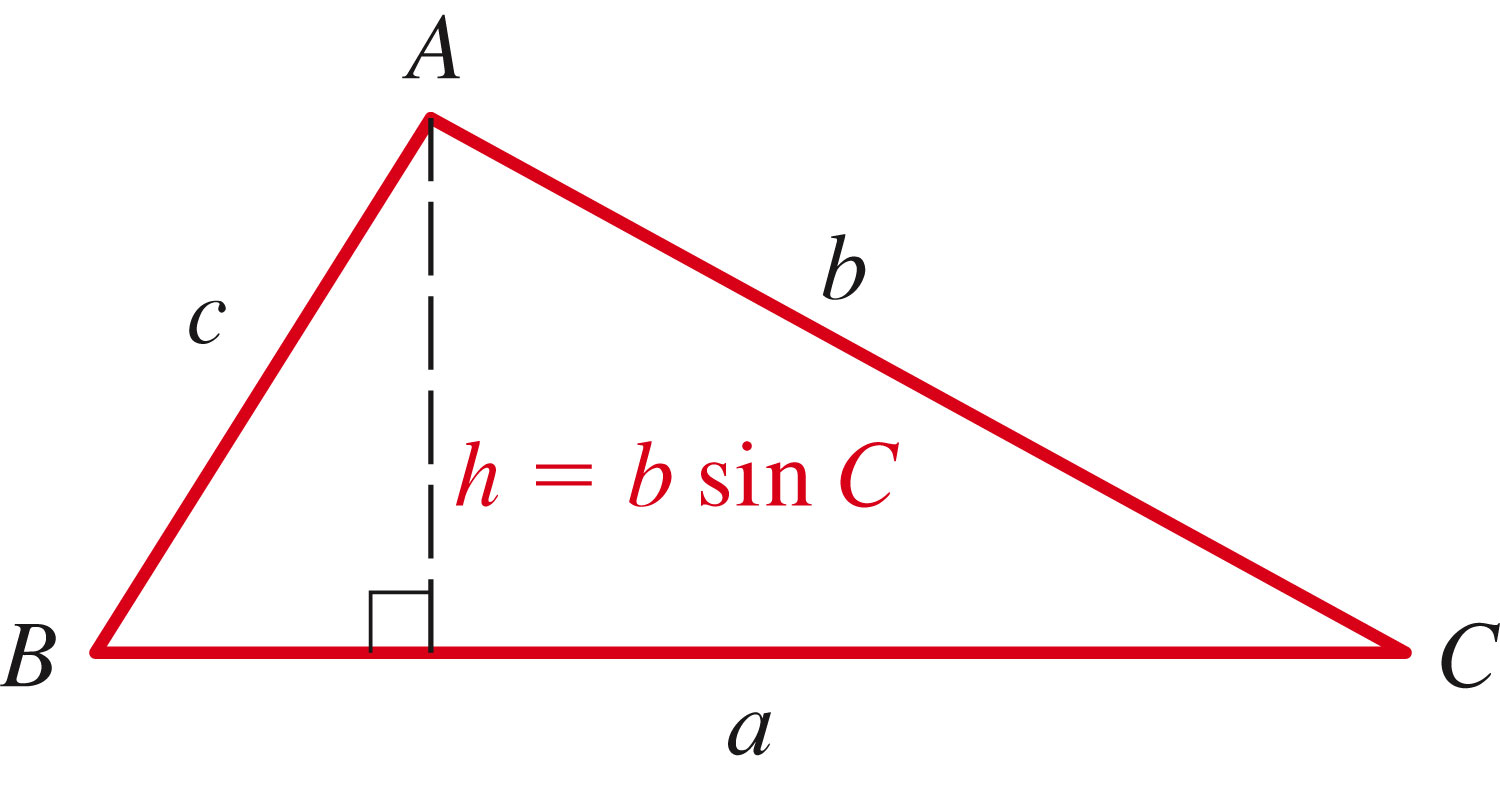
and we can prove this by creating a right triangle and doing some modest area calculations:
ASA, SAA, and SSA are solved with the Law of Sines; the other cases with the Law of Cosines (next section).
Notice that ASA and SAA are actually equivalent, because if you know two angles in a triangle, you know the third. So we can consider this case one where you know a side and all the angles: SAAA.
And while case SAAA is solved unambiguously, case SSA may have either
Examples: