Law of Cosines

The fundamental question is still:

How much information determines a triangle completely (that is, the lengths of the three sides and the interior angles)?

As we've already seen, the four distinct cases we need to consider are

As we've noted before, the case of AAA doesn't appear above, because it cannot be solved (because we don't know the scale -- all the sides could be doubled in length, and the angles would all remain the same).

The first two cases (SAAA and SSA) are solvable (if possible) using the Law of Sines. Now we consider the other two cases: SAS, and SSS.

The law of cosines establishes a relationship between cosines of angles and the lengths of their opposing sides:

${a^2=b^2+c^2-2bc\cos(A)}$

${b^2=a^2+c^2-2ac\cos(B)}$

${c^2=a^2+b^2-2ab\cos(C)}$

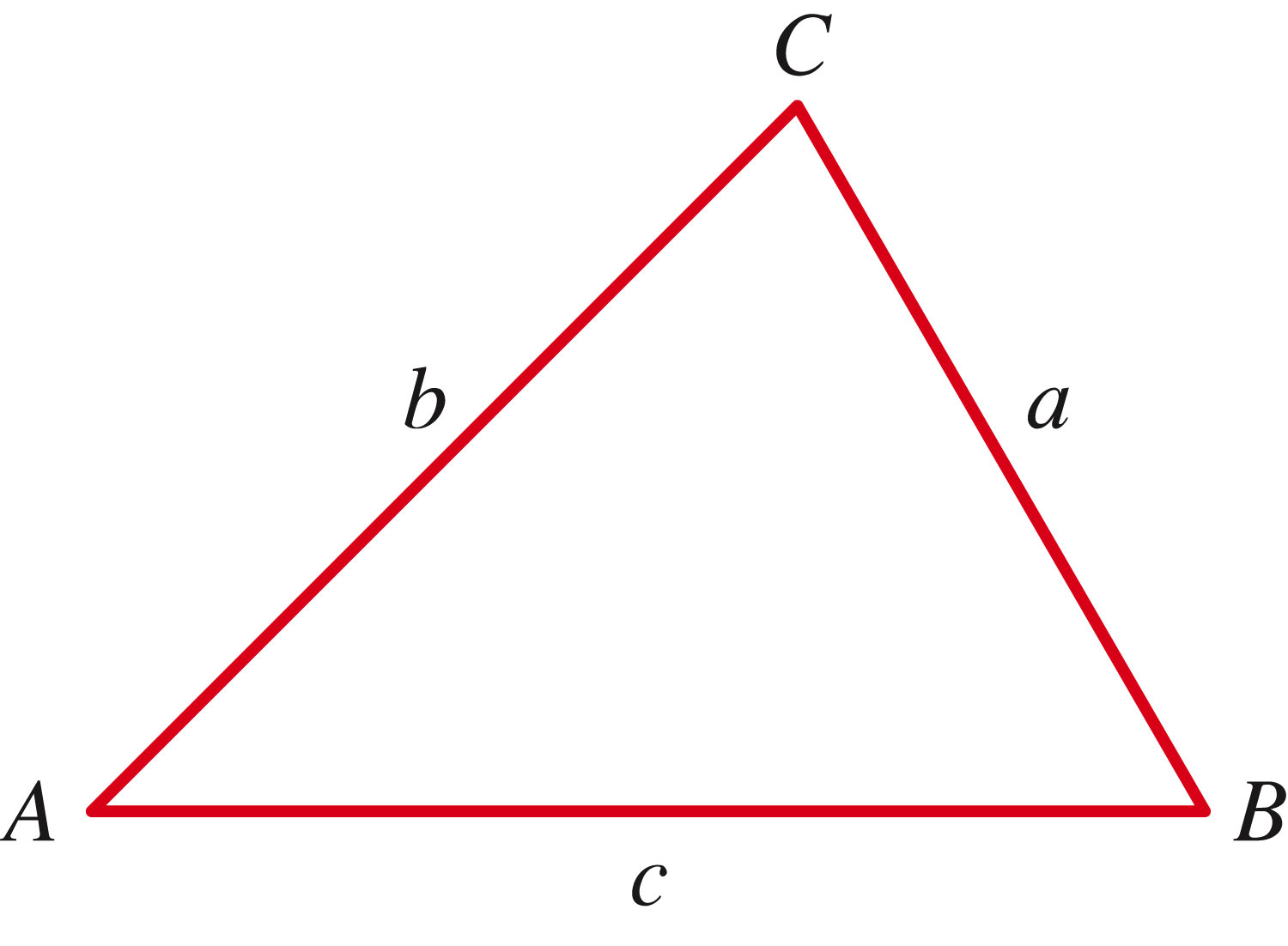
and we can prove this by creating a right triangle and doing some modest calculations:

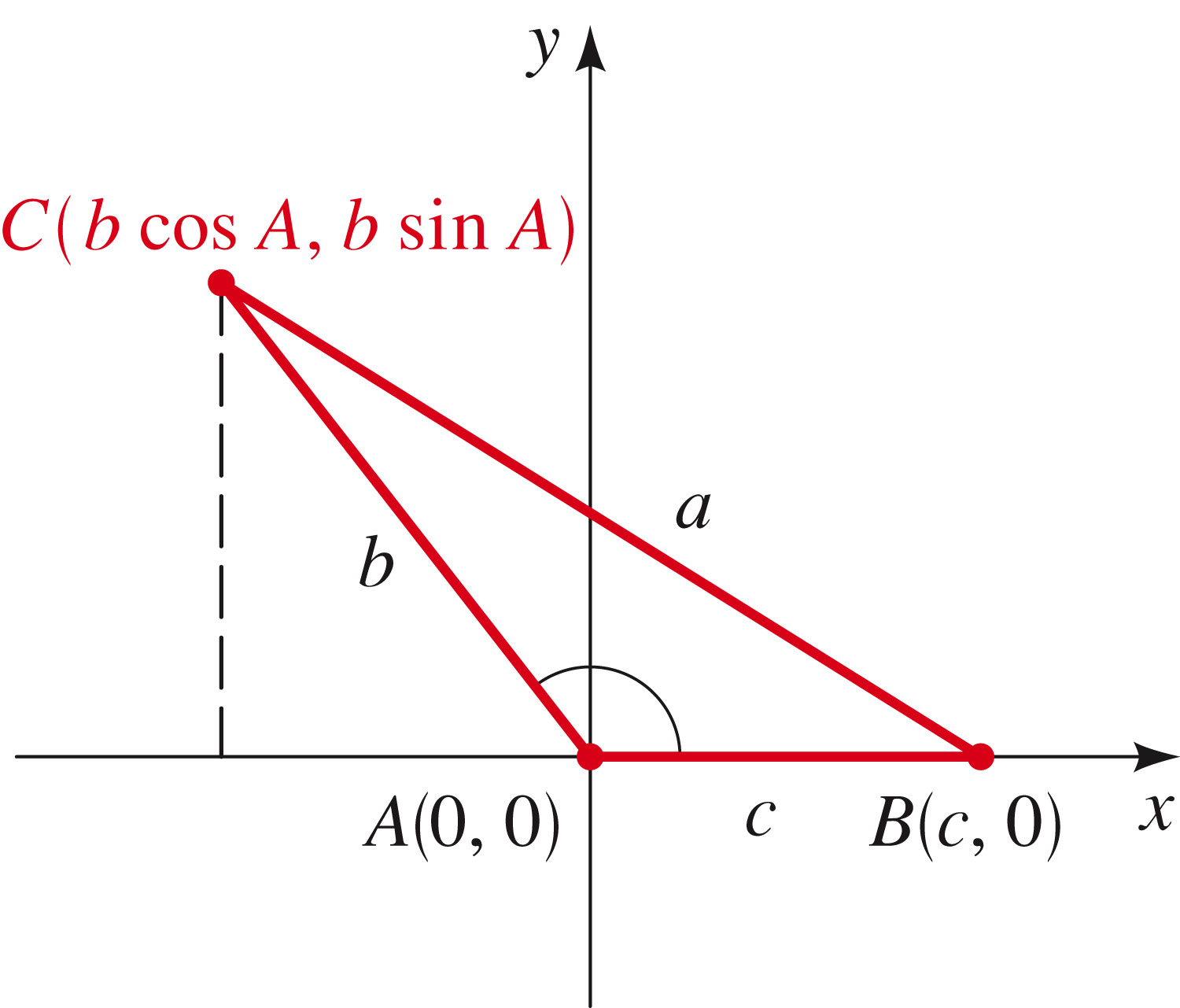
If b and c and angle A are known, then how do we compute a? From the diagram, we can see that a is the hypotenuse of a right triangle, with side lengths ${b\sin(A)}$ and ${c+b\cos(A)}$ . Using the Pythagorean theorem, we see that

${a^2=\left(b\sin(A)\right)^2+\left(c-b\cos(A)\right)^2}$

Squaring this out, we get

${a^2=b^2\sin^2(A)+c^2-2bc\cos(A)+b^2\cos^2(A)}$

and then using the Pythagorean identity ( ${\sin^2(A)+\cos^2(A)=1}$ ) we get

${a^2=b^2+c^2-2bc\cos(A)}$

This is the case of the obtuse triangle. I wonder if you could prove this same thing in the case of the acute triangle:

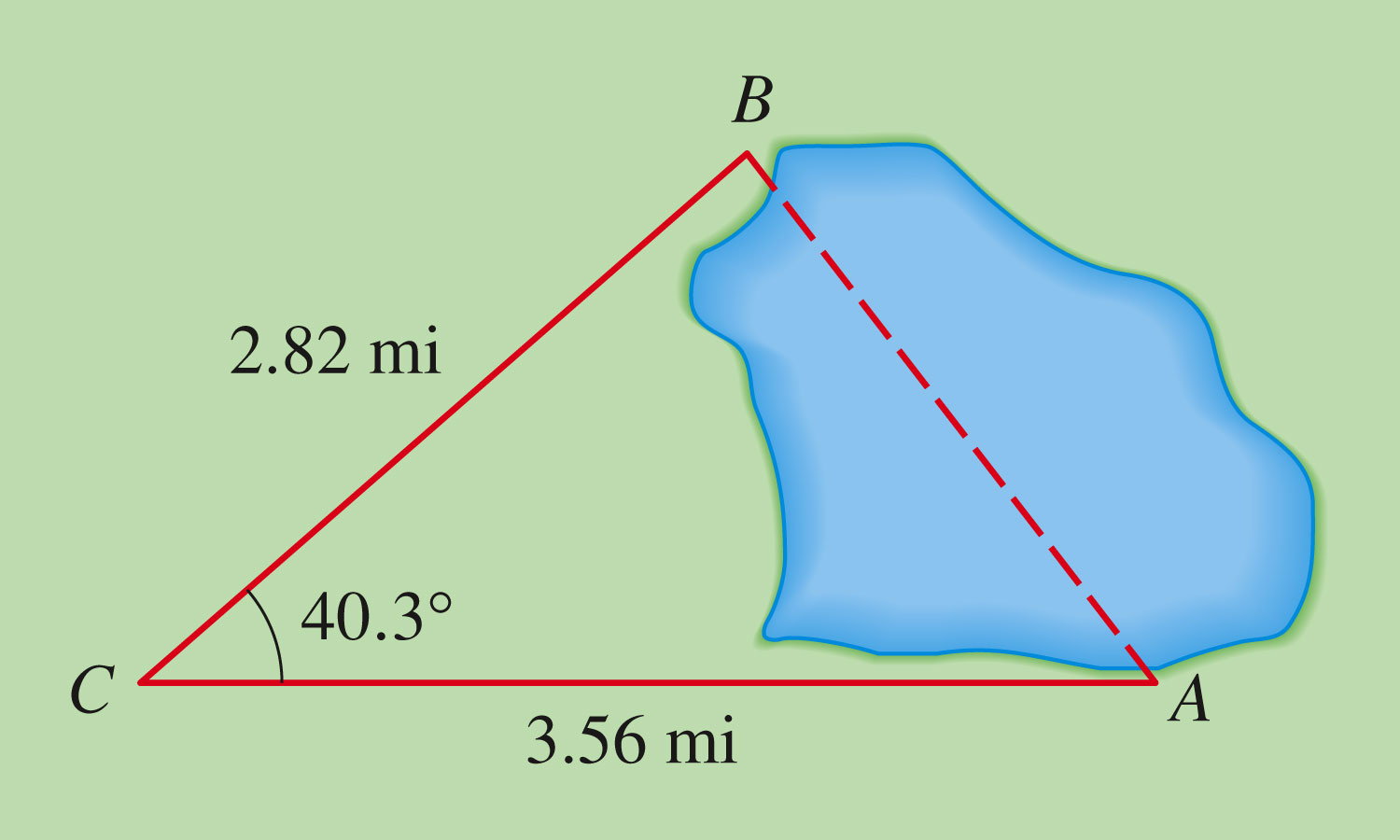
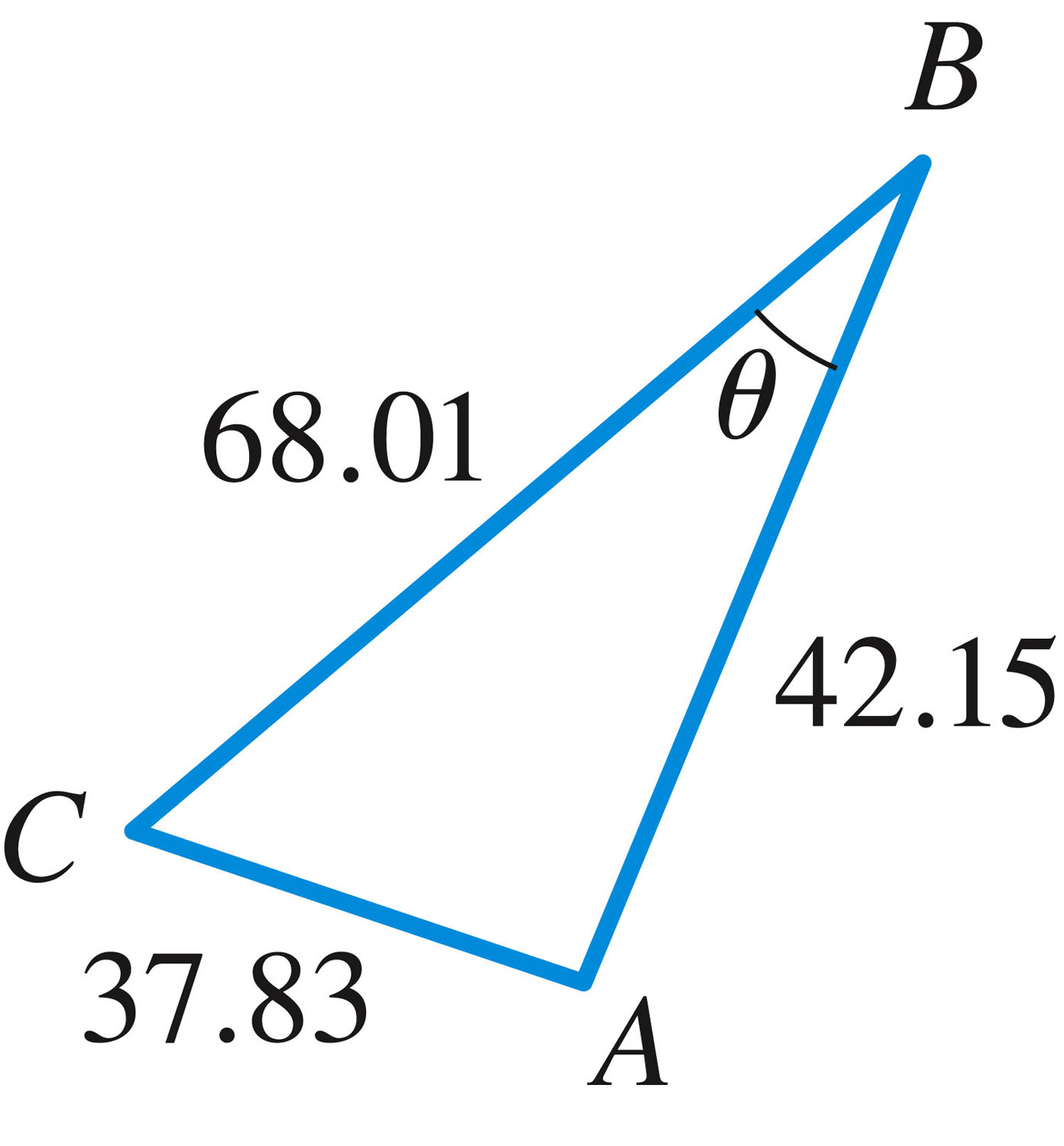
Examples: (Mathematica file)

#39, p. 481:
#7, p. 480:
#14
#45

Website maintained by Andy Long. Comments appreciated.