- basic trig equations (solved by inverse trig functions, and then
periodicity)
- Consider Sine and Cosine: they either have either
- two solutions of
per period (if
),
- one solution per period (if
), or
- no solutions (otherwise):
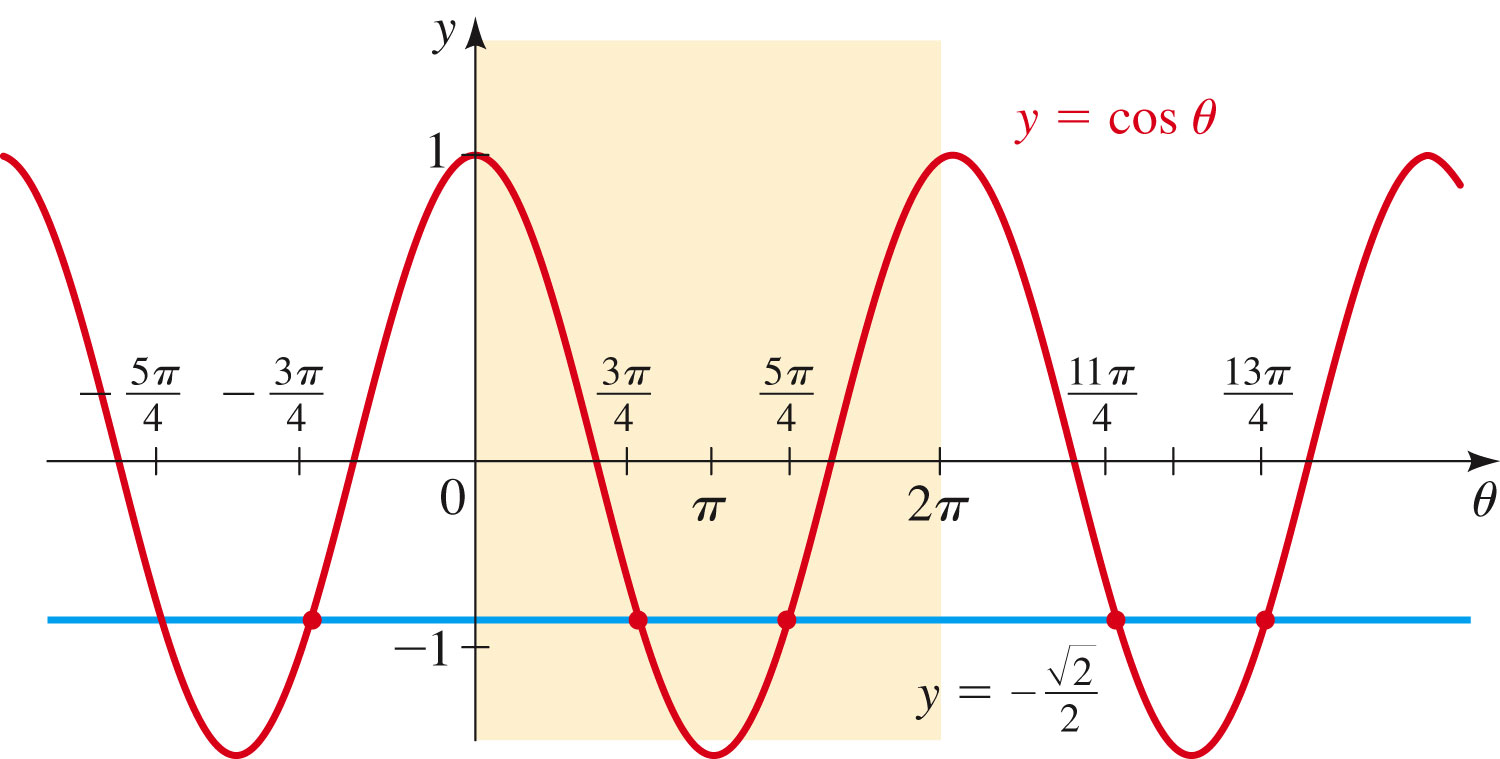
You find the general solution by adding integral multiples of the period to the particular solutions for one period. E.g.
has solutions
and
The general solution is then
and
- two solutions of
- Tangent always has one solution of
per period:
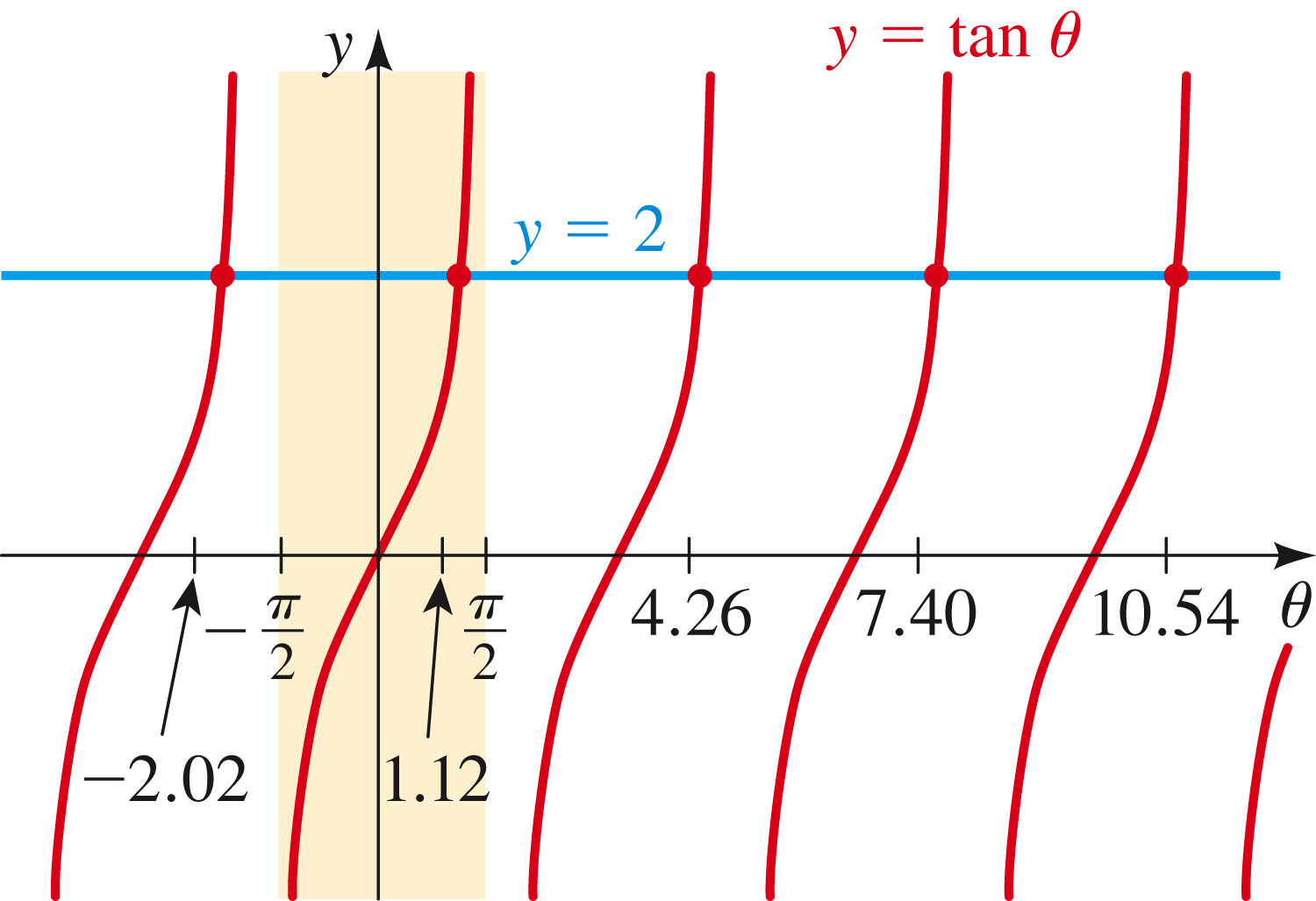
What is the general solution of
?
- Consider Sine and Cosine: they either have either
- trig equations that can be turned into basic trig equations.
- trig equations that are solved by factoring, and relating the solution to other equations you already know. Generally these will eventually involve turning more complicated equations into basic equations somehow.
- #2, p. 522
- #9, #13
- #19
- #32
- #44
- #56
- #57