Transformations

• We'll start off by considering an example. Consider #89, p. 190.

  Note: our author often works "bass ackwards" -- starting with the model and proceeding with the analysis. Usually we start with a data table, proceed to a model, and then make predictions, etc. from there.

1. Upon considering this data, what member of the zoo might you use to fit it?
2. How do we have to modify the function from the "function zoo" to create a model (another, but situation-appropriate function) that will "fit" the data?

Last time we used a graphing calculator to talk about these transformations, with reference to some of the examples. Today we'll try some of them with this applet.

1. Vertical shifts: #21 and 23, p. 187
2. Horizontal shifts: #25 and 27, p. 187
3. Both shifts: #37, p. 188
4. Reflecting Graphs: #29 and 31, p. 187
5. Vertical stretching: #33, p. 187 and 35, p. 188
6. Shifting, stretching, and reflecting: #39, p. 188
7. Horizontal stretching and shrinking: #63, p. 190

The last topic considered in the text is very important: it relates to symmetry. You need to know the definitions of even and odd functions.

An even function has reflective symmetry across the y-axis -- that is, if you reflect the graph across the y-axis you'll get the same graph.

The formula for an even function f(x) will possess the property that

An odd function has rotational symmetry about the origin -- that is, if you rotate the graph 180 degrees about the origin you'll get the same graph.

The formula for an odd function f(x) will possess the property that

Most of the functions in the function zoo possess symmetry.

Exercise: Look at each function in our authors' function zoo, and decide whether it's got symmetry or no (and, if it does, what type?).

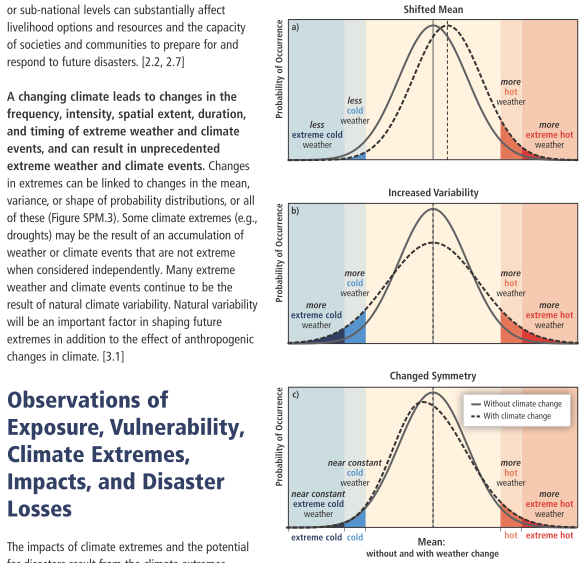
Symmetry is important in many situations. In this report about the connection between climate change and extreme events, one of the discussions is over transformations and symmetry of a distribution model (a function):