-
logarithmic function with base a:
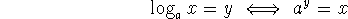
The logarithm is defined as the inverse function of the exponential function, each with base a.
-
natural log: the logarithmic function with base e, denoted
.
-
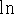The cancellation laws in this particular case lead to the form
for all
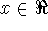, and
for all x > 0. The most important example of these is the natural log and exponential functions, where
for all
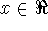, and
for all x > 0.
-
The properties of logarithms are reflections of the properties of exponents:
-
-
It is possible to turn any exponential with base a into a natural logarithmic
function: we can find
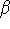such that 
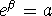by using the inverse
property of the logarithm:
Hence,
and using a property of exponents,
Now we can forget about other bases (hooray!), and work only with base e. Similarly, we can turn a log with another base to the natural logarithm:
Logarithms are the inverse functions of exponential functions. Their graphs are just reflections of the graphs of exponential functions, and many properties are reflected as usual for inverse functions (e.g. the laws of logarithms).
If we understand the natural exponential function 
very well, then it and
its inverse function ( 
) are all we really need to know about exponential
functions (since any other base can be converted into base e). Historically
the bases 2 and 10 have also been important: for example, earthquakes have been
measured on the Richter scale (see exercise #47, p. 434), which uses
- so an earthquake of size 5 has a seismographs wave amplitude 10
times greater than an earthquake of size 4 (this corresponds to about 31 times
more energy - see wwwneic.cr.usgs.gov/neis/general/handouts/richter.html).
Base 2 is very important in the computer world, since computers are based on a
binary arithmatic (it's an on/off world in there!).
If you plan on continuing on in math or science, you would do well to learn these functions inside and out! They're very useful, and will come back to haunt you over and over again.