Day 7, Mat128: Calculus A

What you may not do is use them for anything other than that. If you haven't signed my sheet (and I'm missing a couple of names), please do.

I'd like to make a few comments on individual problems....

We were discussing limits such as \[ \lim_{x \to 2}f(x) \] and so-called "one-sided limits", i.e. \[ \lim_{x \to 2^-}f(x) \] (from the left side) and \[ \lim_{x \to 2^+}f(x) \] (from the right). So we would say here that \[ \lim_{x \to 2^-}f(x)=\lim_{x \to 2^+}f(x)=4 \] and therefore that \[ \lim_{x \to 2}f(x)=4 \]

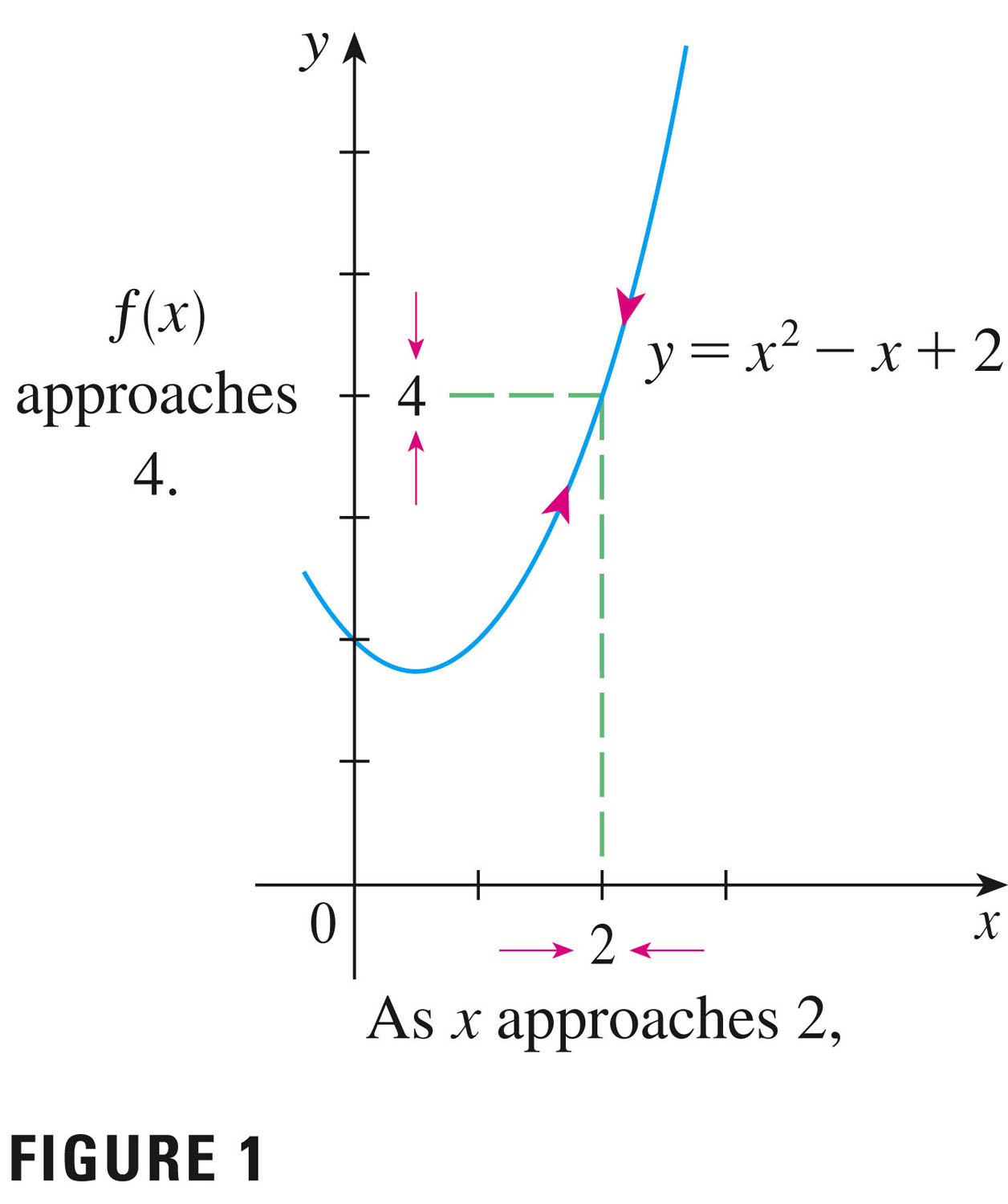
Notice that we approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree.

When we write \[ \lim_{x \to a}f(x) = L \] we assert that we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ (but not equal to $a$).

We say that ``the limit of $f(x)$ as $x$ approaches $a$ equals $L$.'' The intuitive idea is that in the neighborhood of $a$ (down there on the x-axis, around \(a\)), the function $f$ takes on values on the y-axis close to $L$, and those values get closer the closer we get to \(a\).

Questions:

• To what class of functions does $f$ belong in the figure above ("FIGURE 1")?
• Are limits concerned with what happens exactly at $a$?
• If the function is continuous, however (as it is in this case), then the limit is the function value!

• Limits may be infinite (one-sided, perhaps). Here's how we define that:

  infinite limits for $\displaystyle f(x)$ as $\displaystyle x$ approaches $\displaystyle a$: \[ \lim_{x \to a}f(x) = \infty \] means that the values of $\displaystyle f(x)$ can be made arbitrarily large (as large as we please) by taking $\displaystyle x$ sufficiently close to $\displaystyle a$ (but not equal to $\displaystyle a$).

  Similarly we can define \[ \lim_{x \to a}f(x) = -\infty \] and one-sided limits such as \[ \lim_{x \to a^-}f(x) = \infty {\hspace{1.5in}} \lim_{x \to a^+}f(x) = \infty \]

  

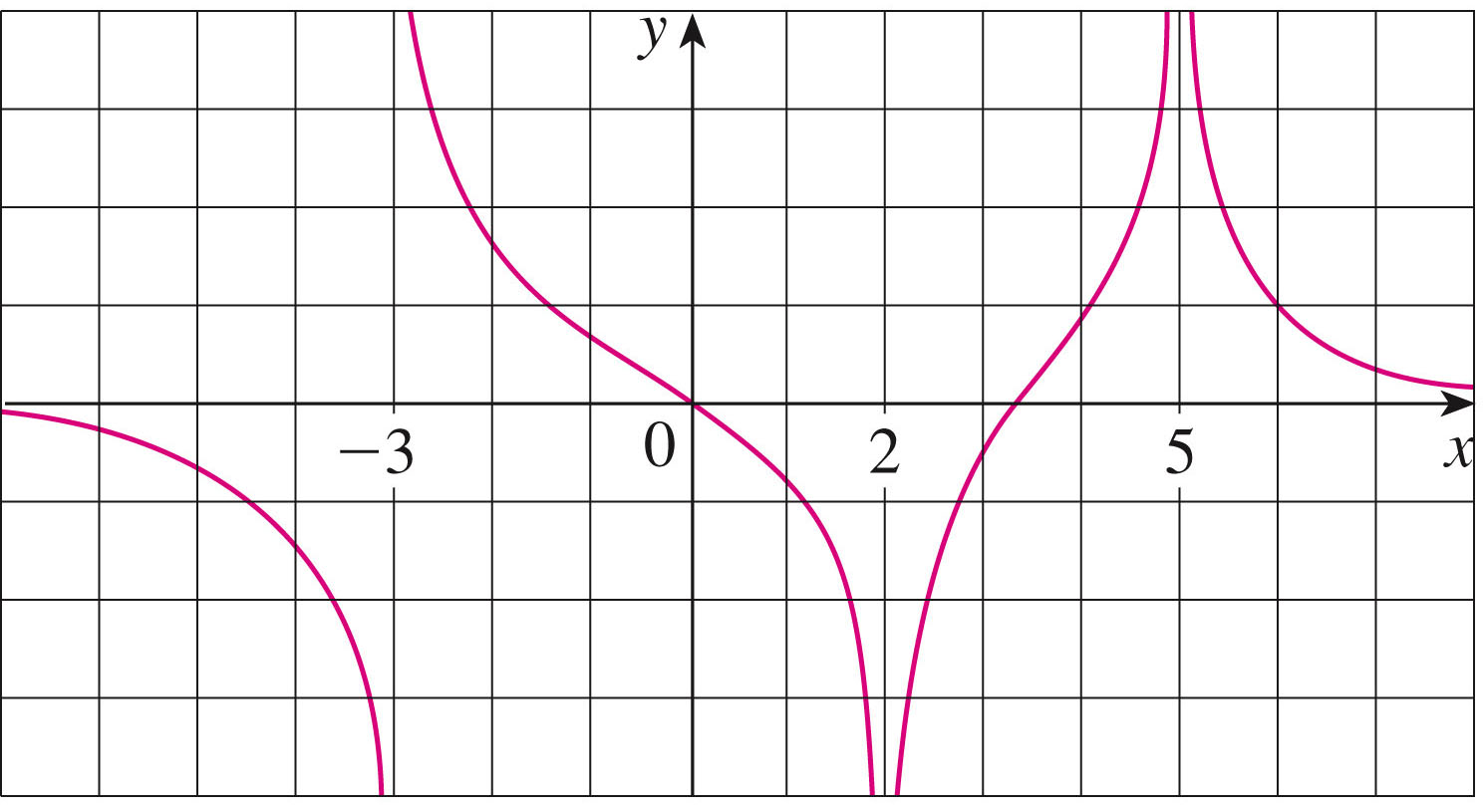
  In any of these cases, we say that \(f\) has a vertical asymptote at $\displaystyle x=a$.

• I handed out a worksheet last time, to help develop your understanding of these limits. Let's take a look at that.

  Desmos can help us investigate that somewhat ugly function....

• Last time (and in this handout) we talked about discontinuity, which is the opposite of "continuity".

  The best case scenario is when the limit exists at a point, the function exists at that point, and the limit is the same as the function value: \[ \lim_{x \to a}f(x) = f(a). \] If that is the case, we say that \(f\) is continuous at \(a\).

  This graph shows us that the function \(g\) is continuous at \(x=-1\):

  \[ \lim_{x \to -1}g(x)=3=g(-1) \]

  

  But this graph also illustrates that there are three things that can go wrong:

  1. The function may not exist at a point (e.g. \(x=2\))
  2. The limit may not exist at a point (e.g. \(x=1\))
  3. The two may exist but not agree. (e.g. \(x=0\))

  Why is continuity in a graph important? We interpret the derivative as the slope of the tangent line (the limit of secant lines!) at a point. You can frequently look at a graph and see where things go awry. For example, if there's no tangent line at a point, then there's no instantaneous velocity! And at any point of discontinuity, it's impossible to create a tangent line (so there will be no derivative).

  Which leads us into our next topic...

• Why are we concerned with "limits"? Here's why:

  The most important definition in calculus is the definition of the derivative (here is the derivative of $f$ at $a$):

  ---

  \[ f'(a)=\lim_{h\to 0}{\frac{f(a+h)-f(a)}{h}} \]

  ---

  And that's why we're so concerned about limits! Memorize this definition. Be able to write it at a moment's notice.

• To see why, let's take a look at the Preview Activity 1.3.1.

• We've seen this idea in another form as well (instantaneous velocity):

  \[ f'(a)=\lim_{x\to a}{\frac{f(x)-f(a)}{x-a}} \]

  This was defined as the slope of the tangent line to a curve (provided the tangent line exists).

• Let's Review a few things, stemming from this "limit definition of the derivative":
  • Function representation -- tables, graphs, algebraic expressions
  • Variables -- independent and dependent. [In the first limit above, the independent variable is actually $h$ for a fixed value of $x$: \(x=a\).]
  • Domains and Ranges
  • Function composition
  • Ratios!
  • Indeterminate things... (division by 0)

    In particular, we're only going to have indeterminacy in our derivative if the numerator goes to 0 when the denominator goes to 0. But that only happens if \[ \lim_{h\to 0}(f(a+h)-f(a))=0 \] This happens when the limit exists, and is equal to the function value. This is equivalent to \[ \lim_{h\to 0}f(a+h)=f(a) \] In order for this to be true, it must be the case that $f$ is continuous at $x=a$.

    We see, therefore, that a derivative exists at $a$ only if the function is continuous there. But not vice versa. A function continuous everywhere does not necessarily have a derivative everywhere -- can you think of one?

  ---

• Now what is our first practical illustration of limits? The calculation of slopes (and thus equations) of tangent lines.

  ---

  The derivative of a function at a point gives the slope of the tangent line there -- provided it exists.

  ---

  We've already seen how the secant lines approach the tangent line for a smooth curve. It's one of the first important problems we'll want to address in calculus. It's why we're interested in limits of things at the outset.

  We usually find the equation of a line using two points, or a point and a slope. The secant line method approaches the tangent line at a point by using a succession of nearby points that are ever closer to the point of tangency:

  Your browser does not support HTML5 Canvas. The secant line method approaching the tangent line (source).

  The tangent ("touching") line osculates ("kisses") the curve at this point.

  Notice the focus on linear functions: linear functions are the most important functions in calculus.

  Once we have the derivative at $x=a$, we can write the equation of the tangent line, graph of linear function $y=T(x)$, using "point-slope" form: \[ y - f(a) = f'(a)(x-a), \] or \[ y = f'(a)(x-a) + f(a). \] It's that simple!