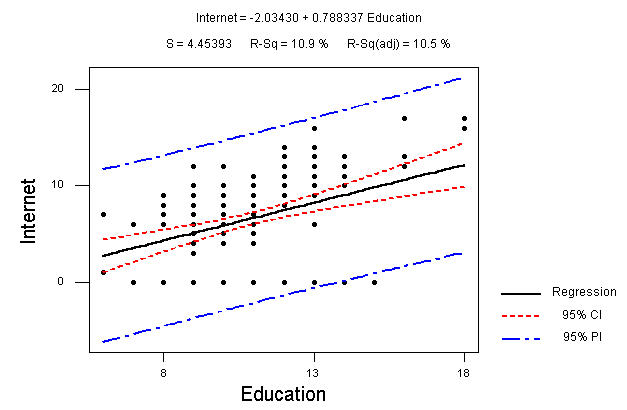
Results for: xr18-08.txt Regression Analysis: Internet versus Education The regression equation is Internet = - 2.03 + 0.788 Education Predictor Coef SE Coef T P Constant -2.034 1.791 -1.14 0.257 Educatio 0.7883 0.1598 4.93 0.000 S = 4.454 R-Sq = 10.9% R-Sq(adj) = 10.5%Here's the picture:

Since the constant term was not significant at an alpha of .05, we might rerun the model without the constant term (under Options, uncheck "Fit Intercept"):
Regression Analysis: Internet versus Education The regression equation is Internet = 0.610 Education Predictor Coef SE Coef T P Noconstant Educatio 0.60969 0.02812 21.68 0.000Because all those zeros mean we have people not participating in the internet, we might decide to change our focus and talk about only those who USE the internet. After removing those people, we obtain a much better model:
Regression Analysis: i_culled versus e_culled The regression equation is i_culled = - 1.39 + 0.950 e_culled Predictor Coef SE Coef T P Constant -1.3878 0.9427 -1.47 0.143 e_culled 0.94967 0.08375 11.34 0.000 S = 2.031 R-Sq = 47.2% R-Sq(adj) = 46.8%Here's the picture:
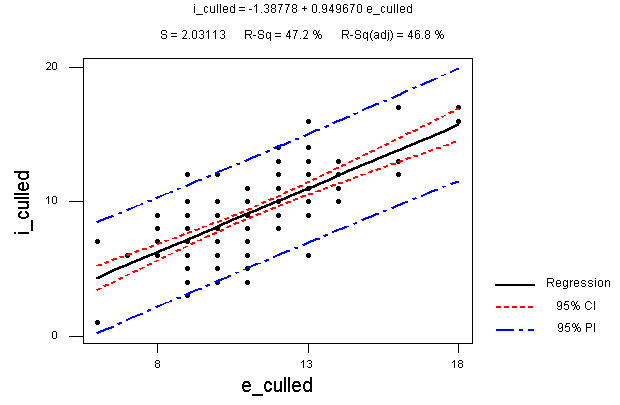
Note that the prediction intervals now are much tighter. This is a much improved model!
Again, the constant is not significant, so we might drop it and rerun the analysis:
Regression Analysis: i_culled versus e_culled The regression equation is i_culled = 0.828 e_culled Predictor Coef SE Coef T P Noconstant e_culled 0.82835 0.01499 55.24 0.000(unfortunately it seems that Minitab doesn't ordinarily produce a fitted-line plot in the case of no constant, although it would be easy for them to do):
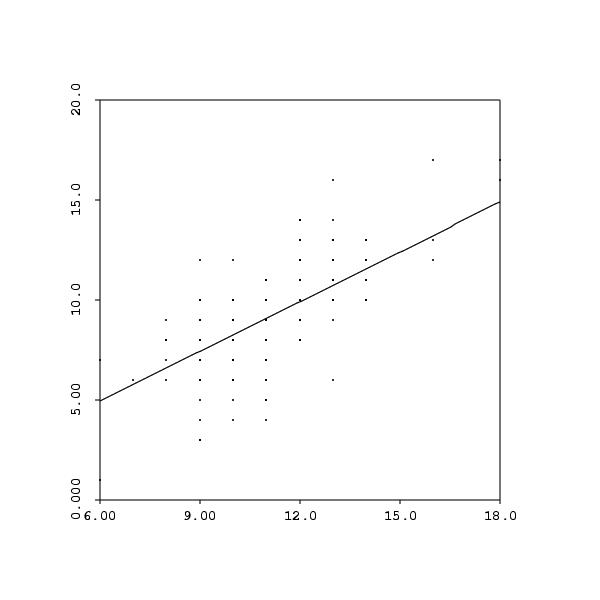
We can now use the model to predict at various points: here's the prediction of internet use for high school graduates (education = 12) and college grads (education = 16):
Predicted Values for New Observations New Obs Fit SE Fit 95.0% CI 95.0% PI 1 9.940 0.180 ( 9.585, 10.296) ( 5.894, 13.986) 2 13.254 0.240 ( 12.779, 13.728) ( 9.195, 17.312) Values of Predictors for New Observations New Obs e_culled 1 12.0 2 16.0The CI is for the average of those years of education; the PI (Prediction Interval) is for a single point. Hence for high school students the mean, based on our data, is between ( 9.585, 10.296) hours with 95% confidence. If your brother just graduated from high school, we might predict with 95% confidence that his use will fall within ( 5.894, 13.986) hours.