Day 3 in Mat229

You're welcome to remind me if it gets to 2:35 and I show no sign of stopping!:)

I used some symbols that folks aren't familiar with:

• Some sets of numbers are given in shorthand:

  These are often given in script, or in bold, or with extra lines drawn in them, e.g. \(\mathbb{Z}\) \(\mathbb{N}\) \(\mathbb{Q}\) \(\mathbb{R}\)

• \(\in\) -- "is an element of". So it is true that \(\pi \in \mathbb{R}\).
• \(\notin\) -- "is not an element of". So it is true that \(\pi \notin \mathbb{N}\).

\(f(x)=49+29*\lceil{x-1}\rceil\)

• A function is invertible on its domain if and only if the function is one-to-one on that domain.

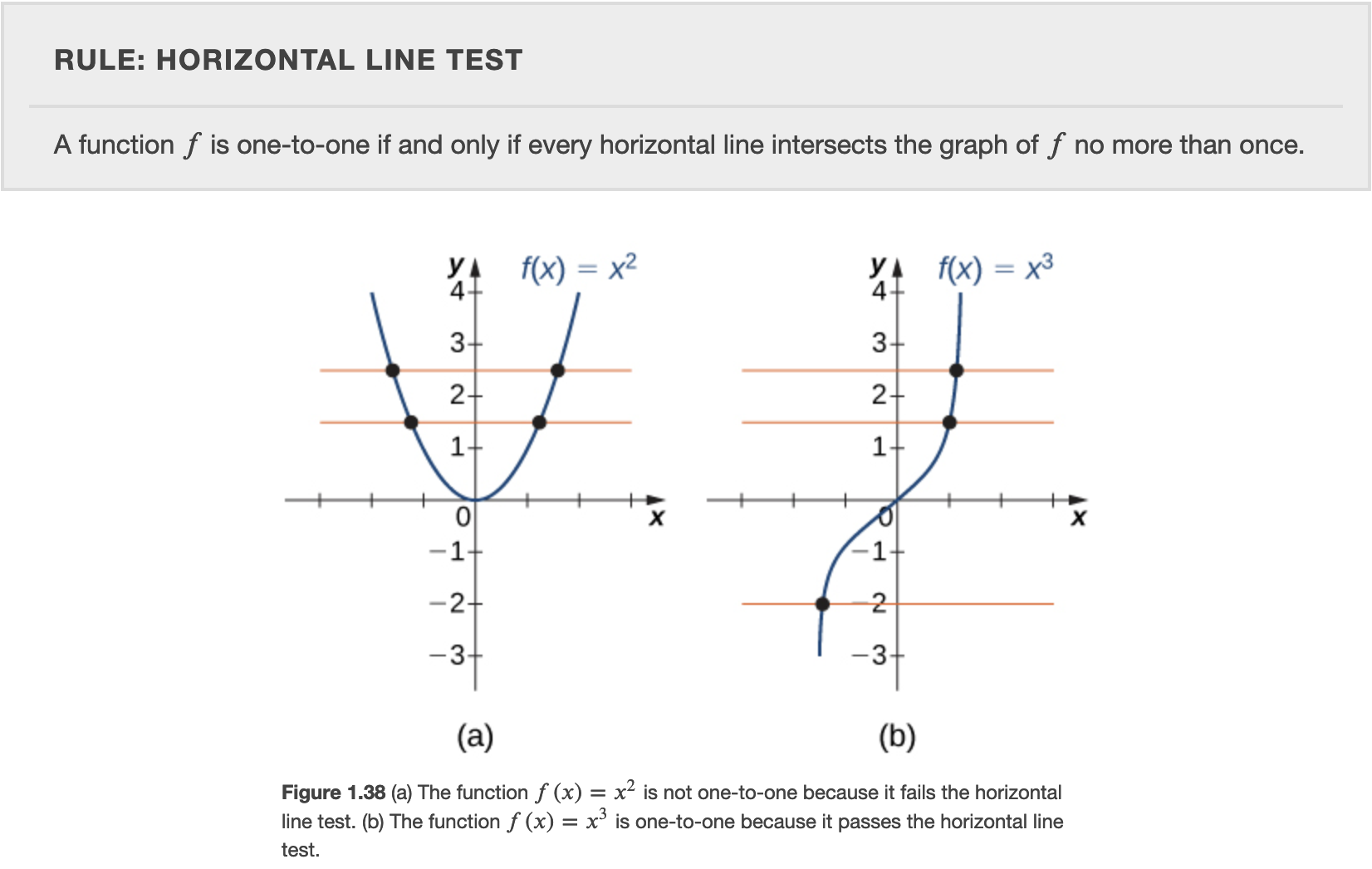
  A function \(f\) is one-to-one provided that no two distinct inputs lead to the same output: \[ f(x_1)=f(x_2) \implies x_1=x_2 \]

  Our authors say it differently, but it means the same thing:

  This says that \[ x_1 \ne x_2 \implies f(x_1) \ne f(x_2) \] Do you see what that's the same thing? (It's called the contrapositive of the first form.)

  I think that the first form leads us more naturally to the horizontal line test:

• The horizontal line test determines whether an inverse even exists (whether the function is one-to-one, which permits its invertibility):
  

• A graphic representing the action of the function and its inverse:
  

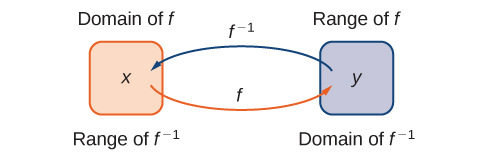
  The important thing to note is that, while the two compositions \[ f^{-1}(f(x)) = x \] and \[ f(f^{-1}(y)) = y \] appear to be very similar, their domains and ranges are reversed: the first composition takes \(x\) back to \(x\), whereas the second composition takes \(y\) back to \(y\).

  One is the "identity function" on the domain, whereas the other is the identity function on the range.

  For you to do: Did you notice the graph of the floor function in your reading?

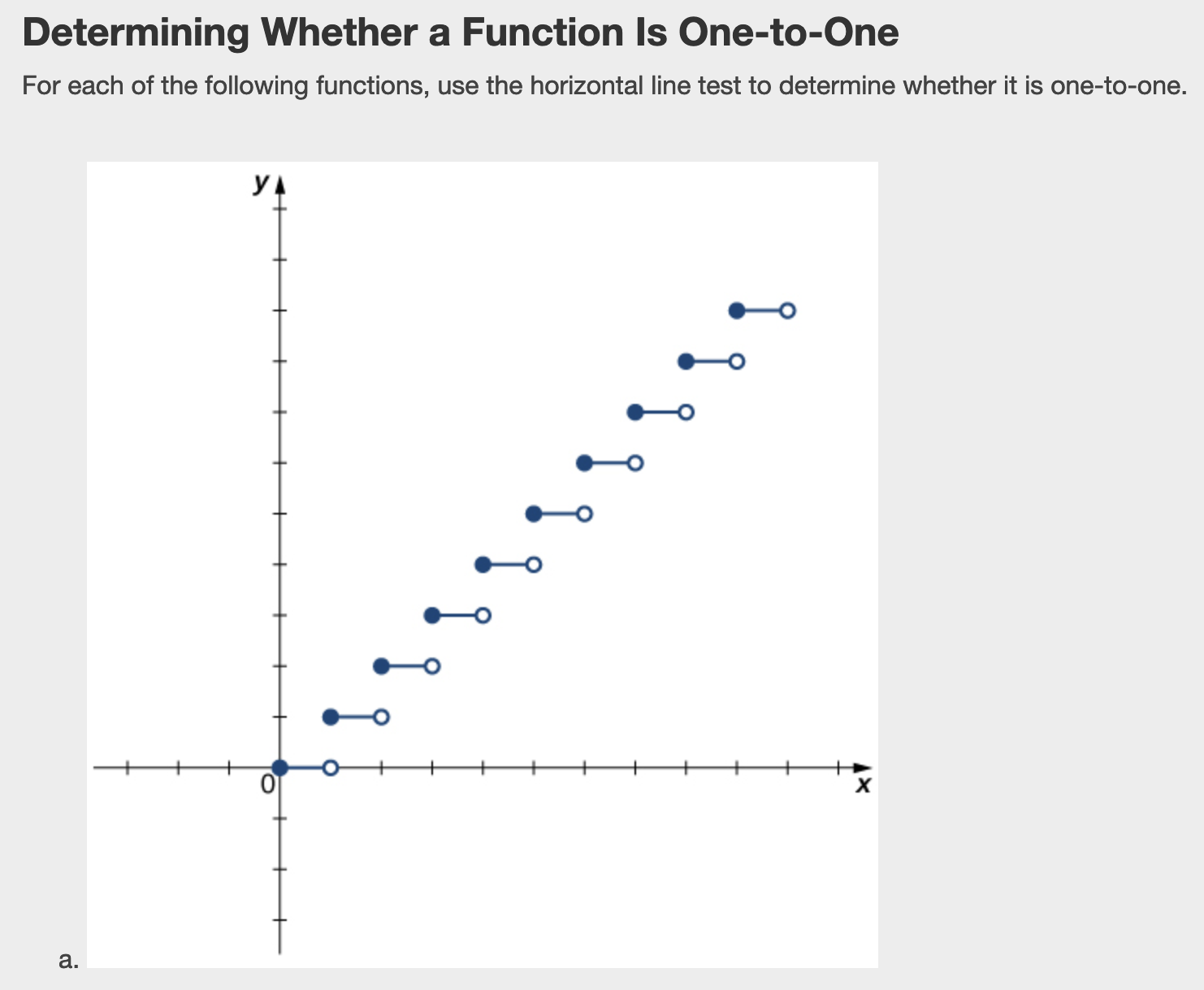
  What is its domain? What is its range? Is it one-to-one? Is it invertible?

• Graphing the inverse is easy if you have the graph of the function itself:
  

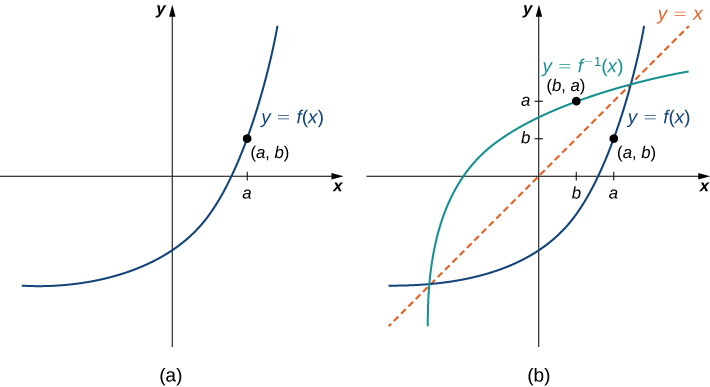
  Just reflect the graph of \(f\) about the mirror line \(y=x\) to get the graph of \(f^{-1}\).

  Notice that wherever the function crosses the mirror, the inverse does at the exact same spot: if you kiss a mirror, the reflection kisses you back!

  For you to do: Let's look at the worksheet, and

  1. Draw the inverse of that first function. Does anyone recognize it? Note where it touches the mirror. Also how asymptotes are reflected.
  2. We can do the two bottom functions on the other side, too: what is surprising about the one on the bottom left? What do we conclude about the function \(f(x)=\frac{1}{x}\)?

• We restrict the domain on non-invertible functions to create an "artificial inverse" in some important cases (e.g. trig functions):
  

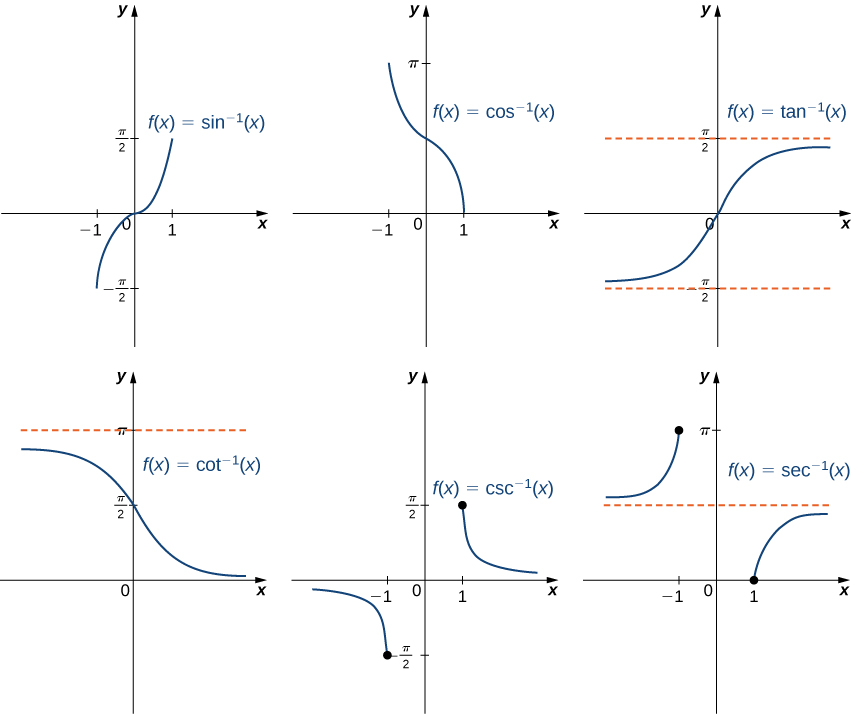
  For you to do: Use your transformation skills to find an identity equation (or maybe two!) linking

  • \(\sin^{-1}(x)\) and \(\cos^{-1}(x)\)
  • \(\tan^{-1}(x)\) and \(\cot^{-1}(x)\)
  • \(\csc^{-1}(x)\) and \(\sec^{-1}(x)\)

  The upshot is that there are really only three distinctively different functions here -- the others are sort of redundant....

• Checkpoint 1.24: domains and ranges of inverses.
• Checkpoint 1.25: sketching the inverse of a linear function.
• Checkpoint 1.26: restricting a function to create an inverse