Number Theory Section Summary: 2.2

The Greatest Common Divisor

``Of special interest is the case in which the remainder in the Division Algorithm turns out to be zero.'' (p. 20)

1. Definitions

   Divisible: An integer b is said to be divisible by an integer , written a | b, if there exists some integer c such that b=ac.

   common divisor: An integer d is said to be a common divisor of a and b if both d|a and d|b.

   greatest common divisor: Let a and b be given integers, with at least one of them non-zero. The greatest common divisor of a and b, denoted gcd(a,b), is the positive integer d satisfying the following:

   1. d|a and d|b
   2. If c|a and c|b, then .

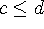   relatively prime: Two integers a and b, not both zero, are said to be relatively prime whenever gcd(a,b)=1.

2. Theorems

   Theorem 2.2: For integers a, b, c, the following hold:

   1. a | 0, 1 | a, a | a
   2. a | 1 if and only if
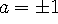
   3. If a | b and c | d, then ac|bd.
   4. If a | b and b | c, then a|c.
   5. a | b and b | a if and only if
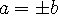
   6. If a | b and 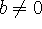, then .
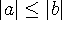   7. If a | b and a | c, then a|(bx+cy) for arbitrary integers x and y.

   Theorem 2.3: Given integers a and b, not both zero, there exists integers x and y such that

   

   Proof:

   Corollary: If a and b are given integers, not both zero, then the set

   

   is precisely the set of all multiples of .

   Theorem 2.4: Let a and b be integers, not both zero. Then a and b are relatively prime if and only if there exist integers x and y such that 1=ax+by.

   (This is just an immediate consequence of Theorem 2.3 - I might have called it also a corollary of Theorem 2.3. It is, however, awfully useful! Don't overlook this one. One reason for calling it its own theorem is that the author wants to hang two corollaries off of this one!)

   Let's look at some examples:

   • 2 and 3
   • 7 and 12
   • 10 and 27 (two non-primes)

   Rough ``Proof'': (using algebra) - just for fun!

   Corollary 1: If gcd(a,b)=d, then gcd(a/d,b/d)=1.

   Corollary 2: If a|c and b|c, with gcd(a,b)=1, then ab|c.

   Theorem 2.5 (Euclid's lemma): If a|bc, with gcd(a,b)=1, then a|c.

   Proof:

   Theorem 2.6: Let a and b be integers, not both zero. For a positive integer d, if and only if

   1. d|a and d|b, and
   2. Whenever c|a and c|b, then c|d.

3. Properties/Tricks/Hints/Etc.

   Whenever we write a|b, we assume that .

4. Summary

   Divisibility is where it's at, and we get our share of it in this section. It's a lot of ``theorem-proof'', but that's good practice! Try to enjoy looking over the proofs, and get into the swing of them.

   In the next section, we'll see how to find the gcd quickly (using the Euclidean Algorithm).