least common multiple: The least common multiple of two non-zero
integers a and b, denoted 
, is the positive integer
m satisfying the following:
- a|m and b|m;
-
If a|c and b|c, with c>0, then
.
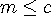Lemma: If a=qb+r, then 
Euclidean Algorithm:
(i.e. 
, so the final remainder is 0). Then
.
Example: (#1/2(a), p. 31) Consider 143 and 227.
- Implement the Euclidean Algorithm using Mathematica.
- Find the gcd.
- Write the gcd as a linear combination of 143 and 227.
Theorem 2.7: if k>0, then
.
Corollary: if 
, then
.
Proof: Let's prove the corollary, without recourse to Theorem 2.7 (which is proved in the process):
Examples: #4a,c, p. 32; #6
Theorem 2.8: For positive integers a and b
One thing this theorem does is give us a method for calculating the lcm (since we can use the Euclidean Algorithm to find the gcd):
Example: #1a, p. 31
Example: #10a,b, p. 32
Corollary: For positive integers a and b
``Gabriel Lamé (1795-1870) proved that the number of steps required in the Euclidean Algorithm is at most five times the number of digits in the smaller integer.''
An improvement to the Euclidean Algorithm is achieved if, instead of choosing
to work with a=qb+r with 
, we work with a=qb+r with |r| <
b/2.
The Euclidean Algorithm gives us a tool for calculating the gcd of two integers. One variation of the algorithm (using ``centered remainders'' from an alternative version of the division algorithm - see problem 7, p. 20) provides a faster algorithm.
The algorithm works by replacing a pair of integers requiring a gcd by a pair of smaller integers, constrained by the fact that the smallest is greater than zero.
The least common multiple (lcm) of two integers is the first positive number appearing in both their multiplication tables, but can be found using the gcd: if they're positive and relatively prime, then the lcm is their product; but if not, then the product divided by the gcd gives us the lcm.
This makes good sense: the gcd is the ``repetitious'' part of the integers.