Diophantine equation: A Diophantine equation is basically one whose solution is over the integers.
Theorem 2.9: The linear Diophantine equation ax+by=c has a solution
iff d|c, where 
. If 
is any particular
solution of this equation, then all other solutions are given by
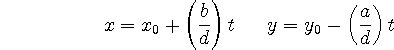
for integral values of t.
Corollary: If 
, and is any particular
solution of the equation ax+by=c, then all other solutions are given by
for integral values of t.
In doing these problems, which are often are of the form of amusing story problems, it is important to include restraints imposed by the nature of the variables. For example, if you are counting roosters, what does a negative number of roosters mean?
Theorem 2.9 is really an obvious conclusion of the corollary of Theorem 2.3:
the set 
is precisely the set of
multiples of , and we're testing whether a value c is
an element of T.
Hence, the question ``Does ax+by=c have a solution?'' is answered by checking to see if d|c (that is, if c is a multiple of d).
A solution is not unique, however, as one can obviously see: for
example, if x=b and y=-a, then ab+b(-a)=0. So for any solution
of
simply add zero (in the form t(ab+b(-a))):
or
also holds true. So 
is a solution, for any integral value of
t.
For those of you who love linear algebra (all of you, I'm sure!), you can think of it this way: if we have a solution
then we can find the solutions of the homogeneous equation
and then tack them on to 
to create the general
solution
This represents all the solutions, if we're willing to allow k to be
real. But we're only interested in solutions over the integers, so we have to
be careful! We can factor out a from the homogeneous
equation, to produce
The safe bet is to make sure that 
: hence the general
solution is
