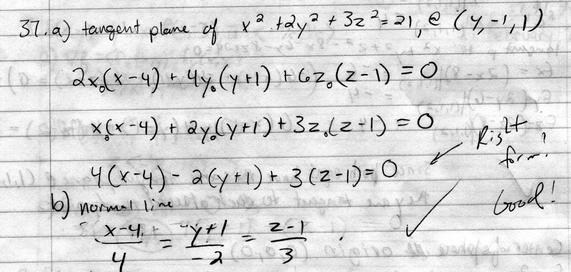
That's a stray mark in front of the y in the normal line equations.
Because this is a tangent plane to a surface at a point, it's my contention that the best representation is that given here,
since it shows the point at which the tangent plane is relevant. It might actually be better to write it as
I prefer the parametric representation of the normal line (which no one used!)
as it shows a point through which the line passes ((4,-1,1), of course!), and a direction vector (the gradient!) to point the way.
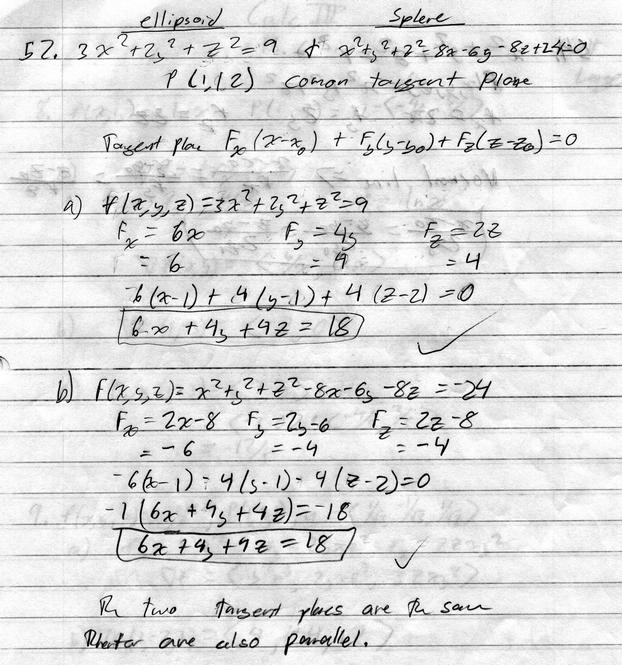
Actually, for this problem the approach the authors was suggesting was perhaps easier: if both surfaces pass through a point and have the same gradient vectors at that point, then the surfaces are tangent. Almost all students acually calculated the equations of the planes.
Just check that both equations are satisfied at P(1,1,2), and that the gradients are the same (or only off by a sign, as in this case: the functions increase in opposite directions).