Day 7 in Mat329

Last time

Next time

Today:

Announcements
- 14.2 problems are due today.
- Your quiz is returned: I want to show you a card trick illustrating one very important aspect of the quiz....
  The second part was about continuity -- you'd already defined a function -- so I was really just looking for $\lim_{(x,y)\to (a,b)}f(x,y)=f(a,b)$.
  In the third part I wanted an application. Why is this mathematics useful?
Today we start section 14.3, on partial derivatives.
Here is "the most important definition in calculus" -- the limit definition of the derivative function, $f'(x)$: \[ f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \]
This is what we want to generalize.
- Take a look at Table 1, p. 925. How can we use the univariate idea?
- What about other directions? Think about a topo map -- you can set off in any direction from a point (often): what does the partial derivative mean in any direction?
- #2, p. 935
So here's the partial with respect to $x$: \[ f_x(x,y) = \lim_{h \to 0}\frac{f(x+h,y)-f(x,y)}{h} \]
We think of $y$ as fixed in this derivative. It's not varying. Only $x$ is varying; is variable.
And here's the partial with respect to $y$: \[ f_y(x,y) = \lim_{h \to 0}\frac{f(x,y+h)-f(x,y)}{h} \]
They're easy to compute, actually: e.g., for $f_x$, just imagine that $y$ is a parameter, and differentiate in the univariate way with respect to $x$.
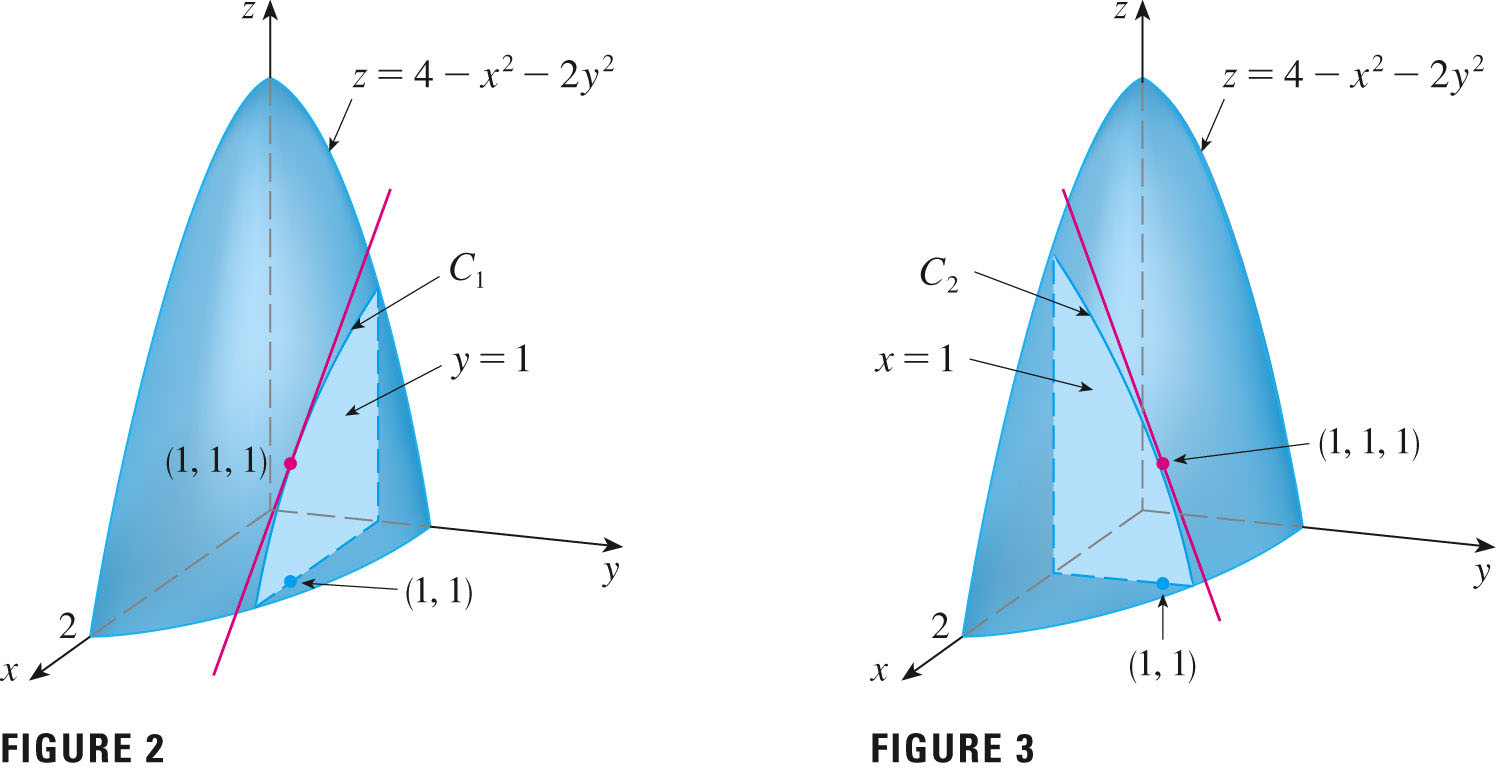
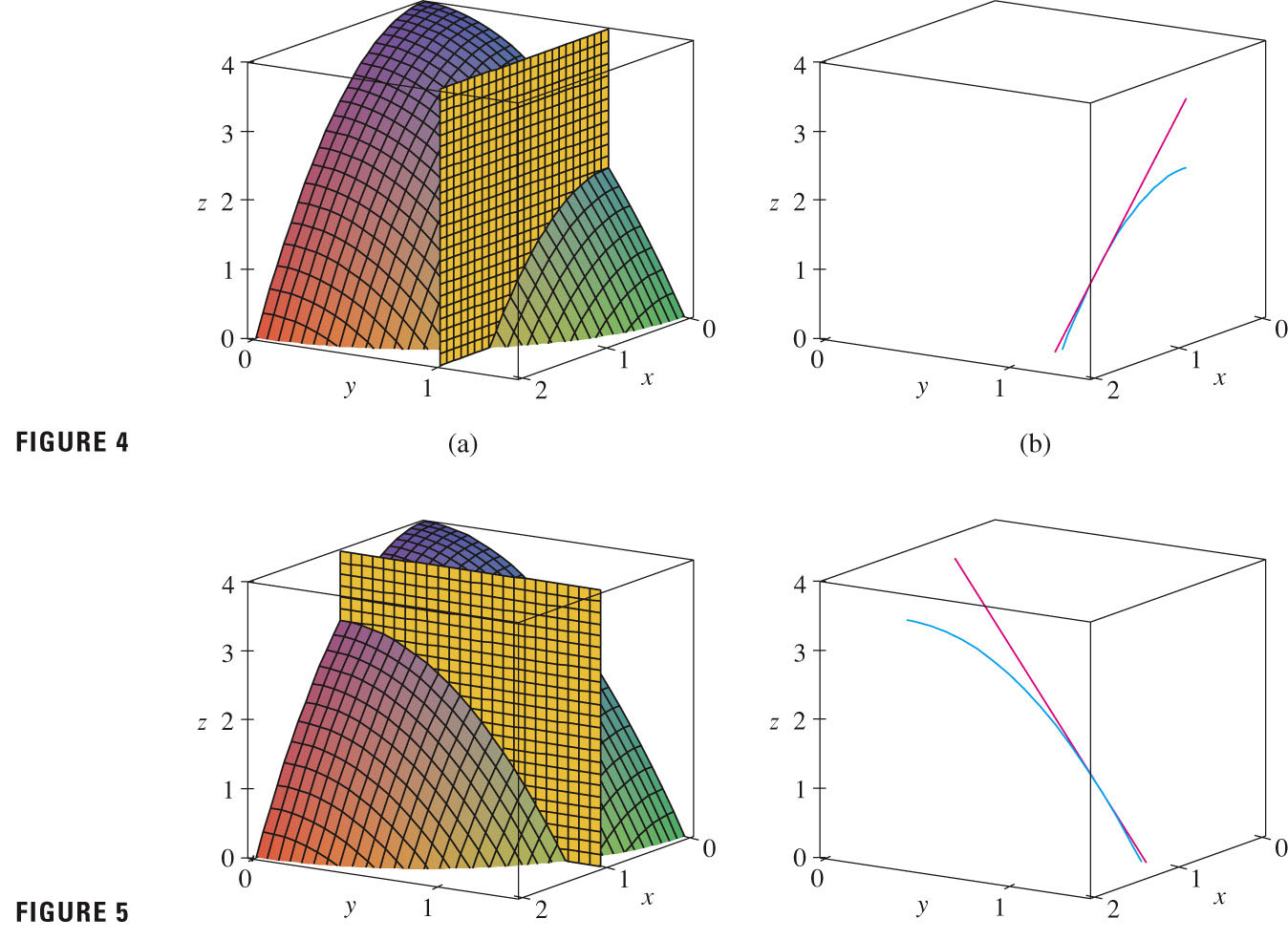
The figures on p. 928 give us this idea very nicely (I hope that my "slicer" from last time does, too).

Problems:
1. #5, p. 936
2. #9
3. #10
4. #21 (first use the limit definition, and then differentiation rules from univariate calculus)
5. #24
Higher partial derivatives are easy to calculate, as well, since each partial is again a multivariate function in its own right. So do it again!
We think of second derivatives in the univariate world as saying something about curvature, and the same is true in the bivariate case.
- #53, p. 937 (note the notation, p. 930)
The world is governed by partial differential equations, such as the heat equation, the wave equation, Laplace's equation, etc.
- #75, p. 937
There is an important theorem in this section: Clairaut's theorem: Suppose $f$ is defined on a disk $D$ that contains the point $(a,b)$. If the functions $\frac{\partial^2 f}{\partial x \partial y}$ and $\frac{\partial^2 f}{\partial y \partial x}$ are both continuous on $D$, then \[ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} \]
- #74, p. 937 (Clairaut's theorem tells us that we don't need to consider $f_{yx}$).

Website maintained by Andy Long. Comments appreciated.