- Sorry, your Lagrange homework isn't graded yet: graded 1, 12, 27
- You have some homework due after the break, on integration.
- We will have a quiz tomorrow.
- Last time we derived the following mask, based on using analogues of the right- and left-rectangle methods to create a trapezoidal rule.
We wondered what would be the relative weight on each depth if we used all four possible methods, and then averaged them?
Recall that the values we are considering are located on the corners of the grid -- not the centers.
1 2 2 2 2 2 1 2 4 4 4 4 4 2 2 4 4 4 4 4 2 2 4 4 4 4 4 2 1 2 2 2 2 2 1 I call this a "data mask", because it fits over the face of the data; each value is weighted by the mask (differentially), based on its position:
Corners are downweighted (used only once), whereas the other edge values get two weights. Interior points get full weight (four) since they're used once in each method.
So we divide these by 4 (because we've added together four different approximations to the depths):
1/4 1/2 1/2 1/2 1/2 1/2 1/4 1/2 1 1 1 1 1 1/2 1/2 1 1 1 1 1 1/2 1/2 1 1 1 1 1 1/2 1/4 1/2 1/2 1/2 1/2 1/2 1/4 Q: Add up the weights, and what do you get? Why?
Then we have to multiply by the areas, of course, to get a volume. To get an average value of the function, we'd divide by the number of subintervals (this assumes, of course, that all subregions have the same area.)
Hopefully these values make intuitive sense to you.
- Warm-ups:
-
Let's estimate average temperature over $[0,4]\times[0,4]$ for #11, p. 992 using
- a midpoint method
- a trapezoidal method
- Take a look at Example 4, p. 1003: how would we do the same
problem using the trapezoidal rule?
-
Let's estimate average temperature over $[0,4]\times[0,4]$ for #11, p. 992 using
- Problems:
- #6, p. 1005
- Suppose the figure below represents depths. Produce an
average value over the 3x4 regions in the center the image:
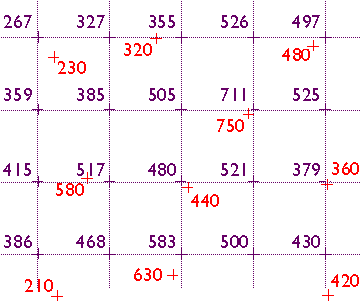
In Example 4, we turned contour into grid: could you turn this grid into a contour map?
- Just FYI: Another way to derive the trapezoidal rule
- Some homework help
Let's try to generalize the univariate methods we know. There's some good news in section 15.2 (Fubini's theorem): in most cases, we're going to be able to do iterated bivariate integrals by doing twice the work of univariate integrals, using a process that one might call "partial integration" (in analogy with "partial differentiation").
Fubini's theorem: If $f$ is continuous on the rectangle $R=\{(x,y)|a\le{x}\le{b},c\le{y}\le{d}\}$ then \[ \int\!\!\!\int_{R}f(x,y)d A = \int_{a}^{b}\int_{c}^{d}f(x,y)dydx = \int_{c}^{d}\int_{a}^{b}f(x,y)dxdy \] This is true even if $f$ is merely bounded on $R$, $f$ is discontinuous only on a finite number of smooth curves, and the iterated integrals exist.
Follow the infinitesimals to know which dummy variable of integration to work with first -- e.g. the order of $dx dy$ is very important in an integral, because it indicates which limits pertain to which variable.
Separable integrals are very nice to work with -- that is, if the integrand is a product of two functions $g(x)$ and $h(y)$, we can simply do two univariate integrals:
\[ \int_a^b\int_c^df(x,y)dydx=\int_a^b\int_c^dg(x)h(y)dydx= \int_a^b g(x)dx \int_c^d h(y)dy \]
- #1, p. 1011
- #6
- Integrate a plane over a rectangular region and what do you get? (Compare the trapezoidal method, and the midpoint method.)
- #15 (two ways)
- #26