- You have an exam next week, Thursday, which will cover through 15.4.
-
Last time we started by taking a look at Example 2, p. 1024,
to identify the problem(s):
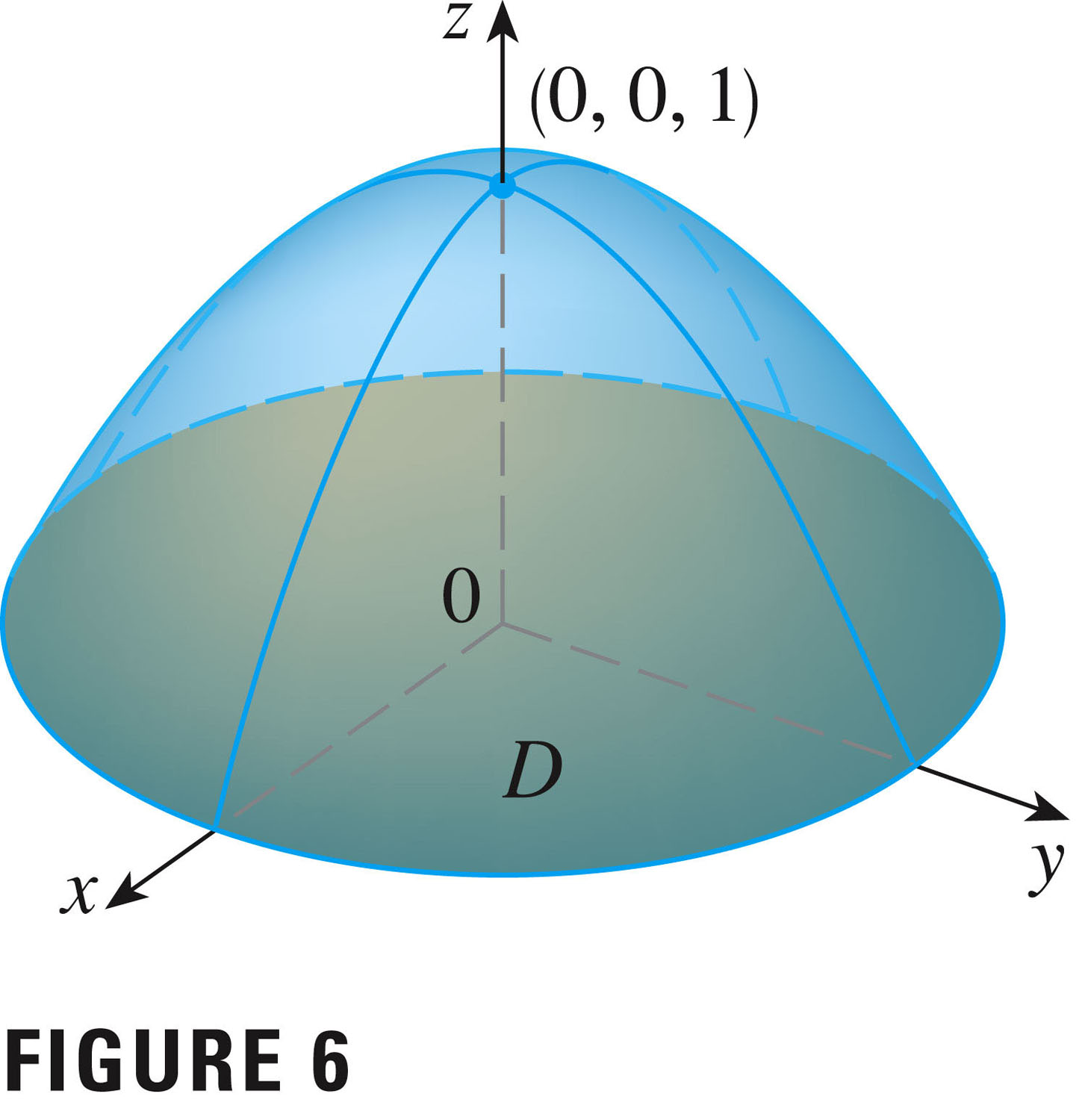
- Changing to polar coordinates isn't too bad: we just switch from
describing our region using Cartesian coordinates $x$ and $y$, and move
to polar coordinates $r$ and $\theta$, via the transformation equations
\[
r^2=x^2+y^2 \hspace{1in}
x=r\cos{\theta} \hspace{1in}
y=r\sin{\theta}
\]
For "Polar rectangle" $R=\left\{ (r,\theta)\
|\ a\le{r}\le{b},\ \alpha\le\theta\le\beta\right\}$, substitution gives
\[
\int\!\!\!\int_{R}f(x,y)dA =
\int_{\alpha}^{\beta}\int_{a}^{b}f(r\cos(\theta),r\sin(\theta))r dr d\theta
\]
Notice that the differential of area, $dA$, has been replaced by $r dr d\theta$: take a look at Figures 3, 4, and 5, p. 1022/23:
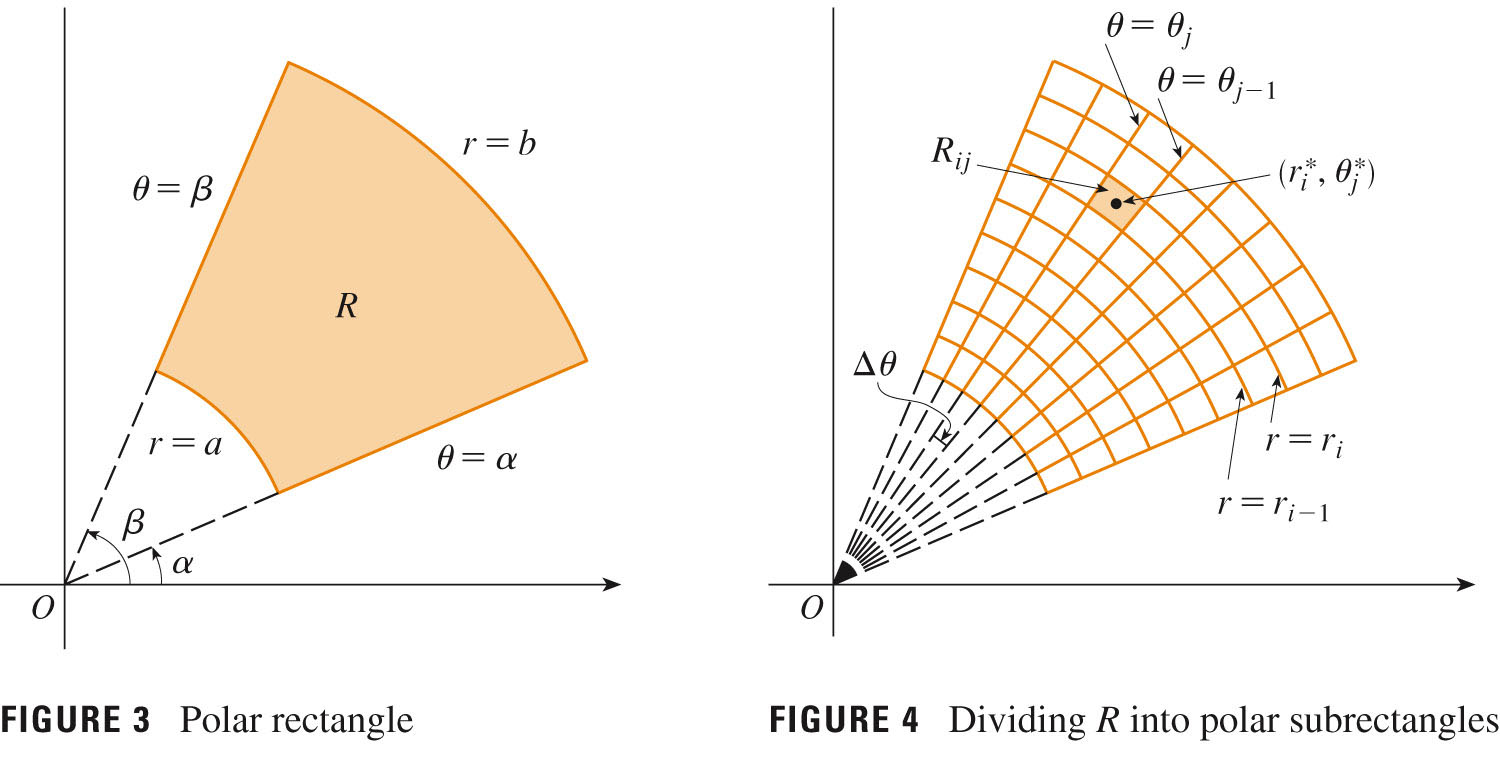
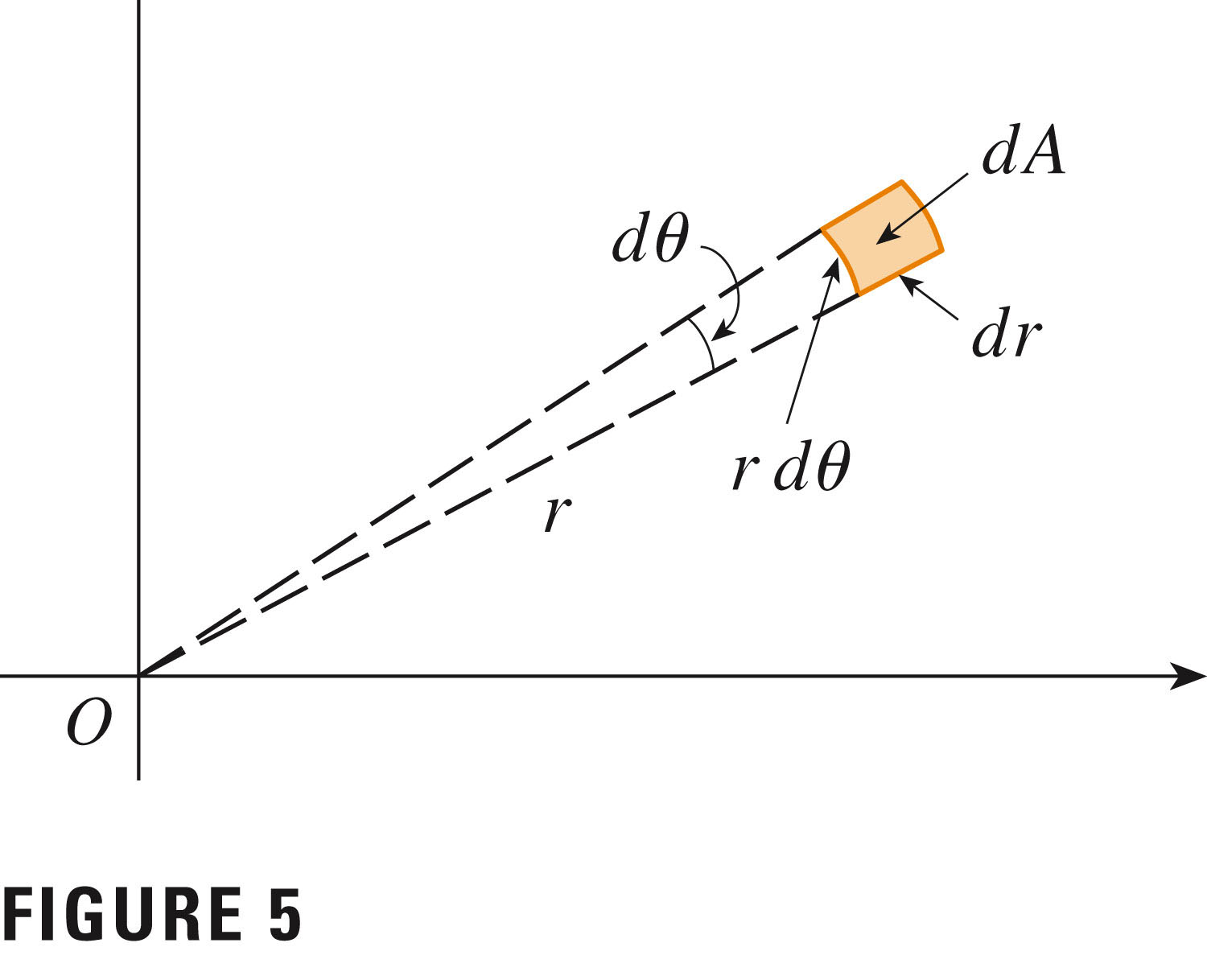
I jokingly refer to this as pirate integration: that "r dr" is too much fun!
- Examples:
- Problems 1-4, p. 1026
- #5 (why does the integral represent the area?)
- #10
- #14 (a little more complicated, and we'll just set it up so that you can practice your univariate integrals!:)
- #36 (and the important question: how should the nozzles be designed so that you deliver a constant amount of water per hour at every point in the field? Wouldn't that make sense?)
- We're stepping up the dimension -- no big deal, but we've got more
work to do. Sometimes it's just three times as much work (as when we
have a separable function, a product of three functions
$f(x)g(y)h(z)$).
The volume element in rectangular coordinates is $dV=dxdydz$, as expected. An infinitesimal box.
- Examples:
- What's the average temperature in a special empty
rectangular room, where
- Walls are perfectly insulated
- Floor is kept at constant temperature of 77 degrees F.
- Ceiling (10 feet above) is kept at constant temperature of 70 degrees F.
- Temperature equilibrates (is steady in time)
- #9, p. 1049
- #20, p. 1049 (this is a volume of rotation from your univariate calculus days -- you might try using disks or shells to find the volume "the old fashioned way".)
- #33, p. 1050 (writing the integral in different ways)
- #24, p. 1049
- Some applications from physics and stats:
- #49
- #52 (separable)
- What's the average temperature in a special empty
rectangular room, where