Day 33 in Mat329

Last time

Next time

Today:

Announcements
- Tests aren't graded yet. I haven't looked at them -- should I?:)
- Your 15.4 homework is returned: graded 17, 28, 35
  - Draw more pictures.
  - Zach and Tommy nailed #35!
  - For those of us who didn't nail #35, the sooner that you notice that $\int_{0}^{2\pi}\sin(x)dx=0$, the better (integrating over a period of a trig function, sine or cosine, equals zero -- or any multiple of periods).
- Your 15.7 homework is due next time.
How are you doing on the triple integrals? What questions do you have?
We're going to keep moving, into section 15.8: Cylindrical coordinates represents one generalization of polar coordinates: \[ x=r\cos{\theta} \hspace{1in} y=r\sin{\theta} \hspace{1in} r^2=x^2+y^2 \hspace{1in} z=z \] So it represents a polar coordinate transformation for two coordinates, and leaves $z$ untransformed.
The volume element ($dV$) is given by $rdrd{\theta}dz$, as one can see in Figure 7, p. 1054:

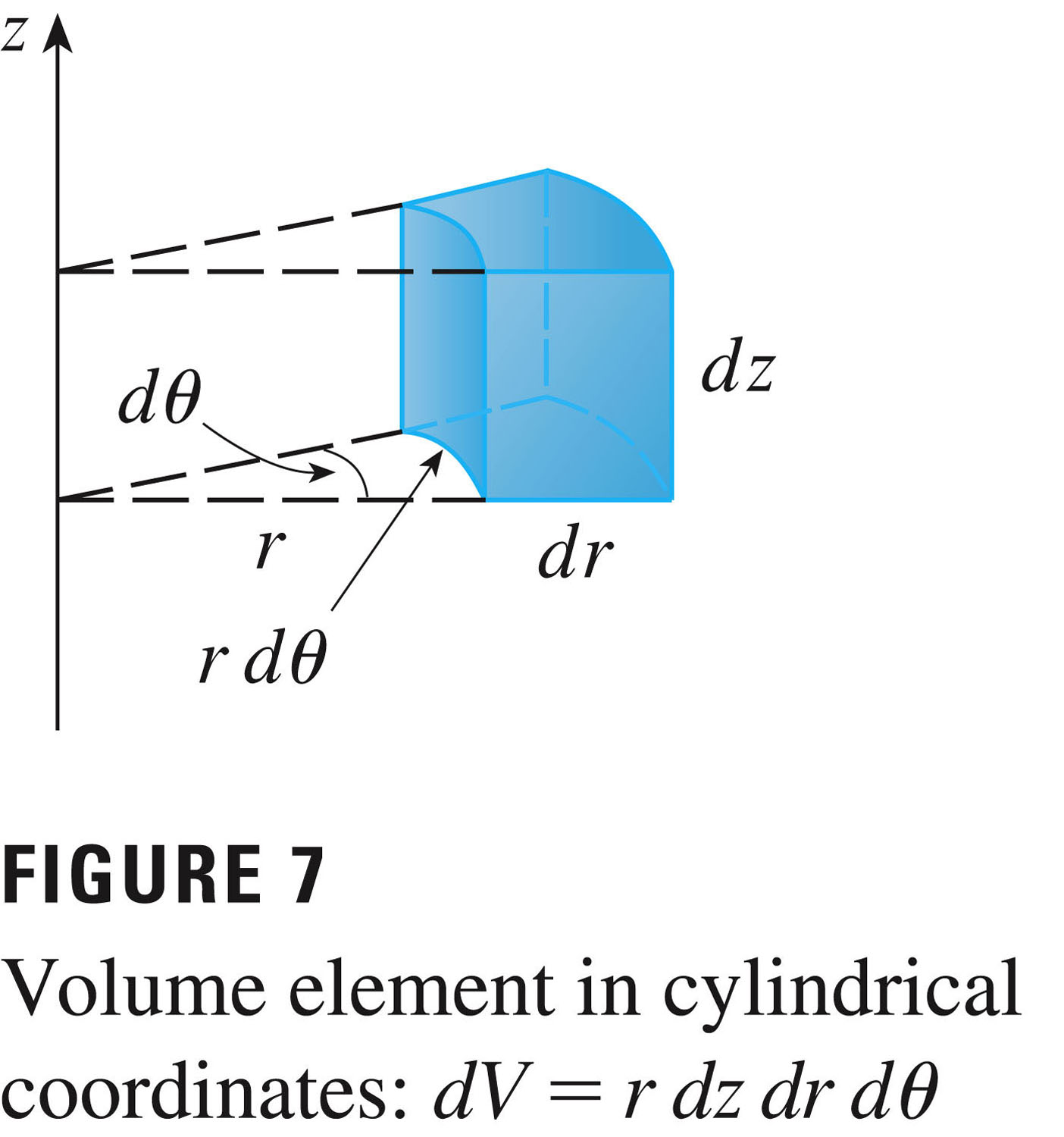
This is a simple generalization of the polar formula of the area element $dA$.
Examples:
- #1, p. 1055
- #3
- #13
- let's revisit the problem, #20, p. 1049.
- #26
- Then we'll try #31 -- Mt. Fuji!

Website maintained by Andy Long. Comments appreciated.