Day 40 in Mat329

• Let's make your 16.2 homework due Friday.
• Your 16.1 homework is returned: graded 18, 26, 36
  • Michael Booth
  • Zach
  • Nathan
  • #18: at the origin is the zero vector; symmetry
  • #26: Mikael Soto noticed the key element; express the gradient in polar coordinates, and what do you get?
  • #36: the vector field is a velocity field (and "i before e except after c!":)

• Your quiz is returned, too.

  Elizabeth mentioned that the quiz was a homework problem...

• The line integral of $f$ along $C$ is \[ \int_{C} f(x,y)ds = \lim_{n \to \infty}\sum_{i=1}^{n}f(x_i^*,y_i^*) \Delta s \]
  

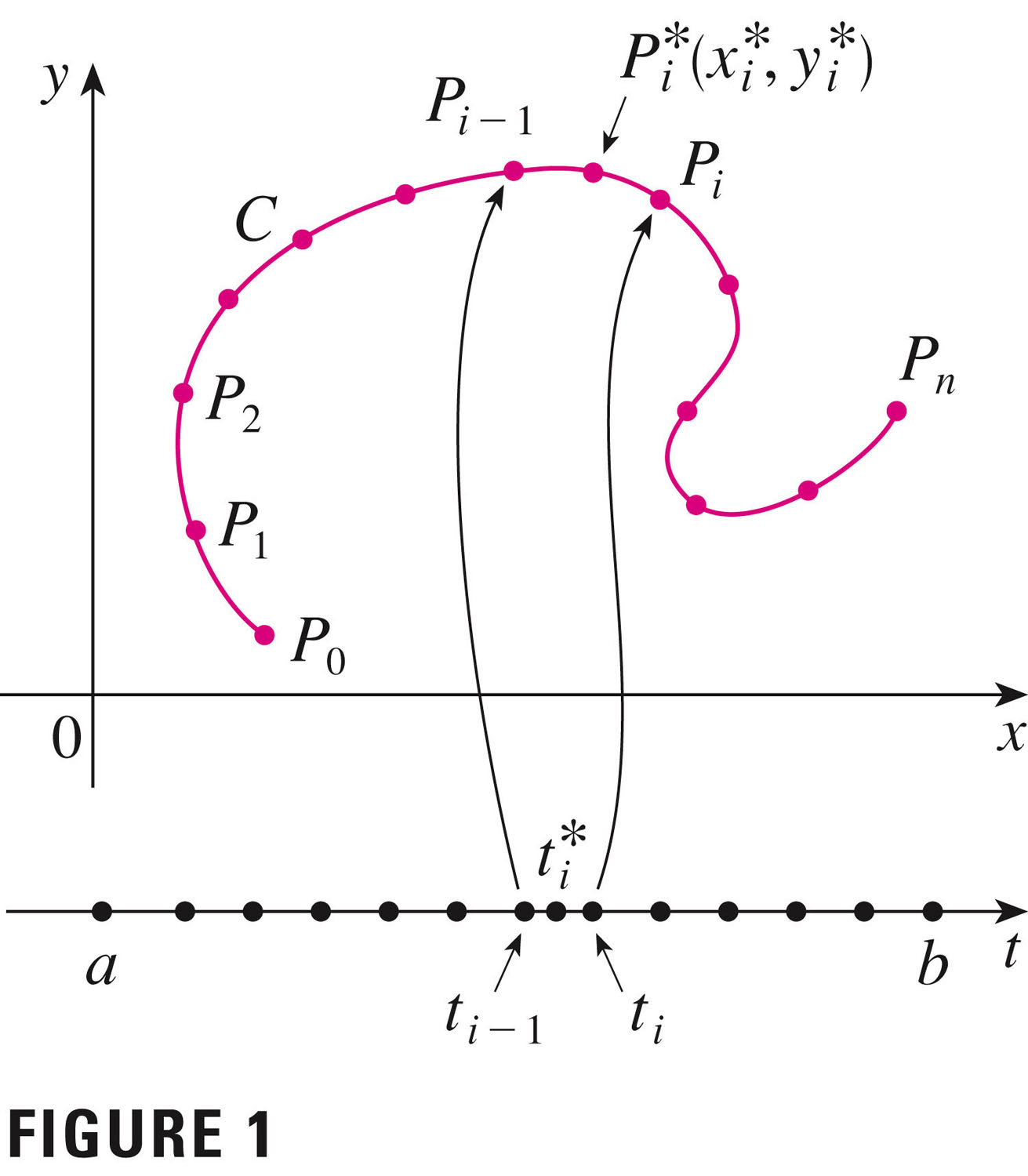
• If $f$ is continuous, then \[ \int_{C} f(x,y)ds = \int_{a}^{b} f(x(t),y(t)) {\sqrt{\left(\frac{dx}{dt} \right)^2 + \left(\frac{dy}{dt} \right)^2 }} dt \] and this is independent of the parameterization $(x(t),y(t))$ (provided the curve is traversed just once) as $t$ increases from $a$ to $b$.

  We can think of this as an area, per Figure 2 (if $f$ is positive):

  

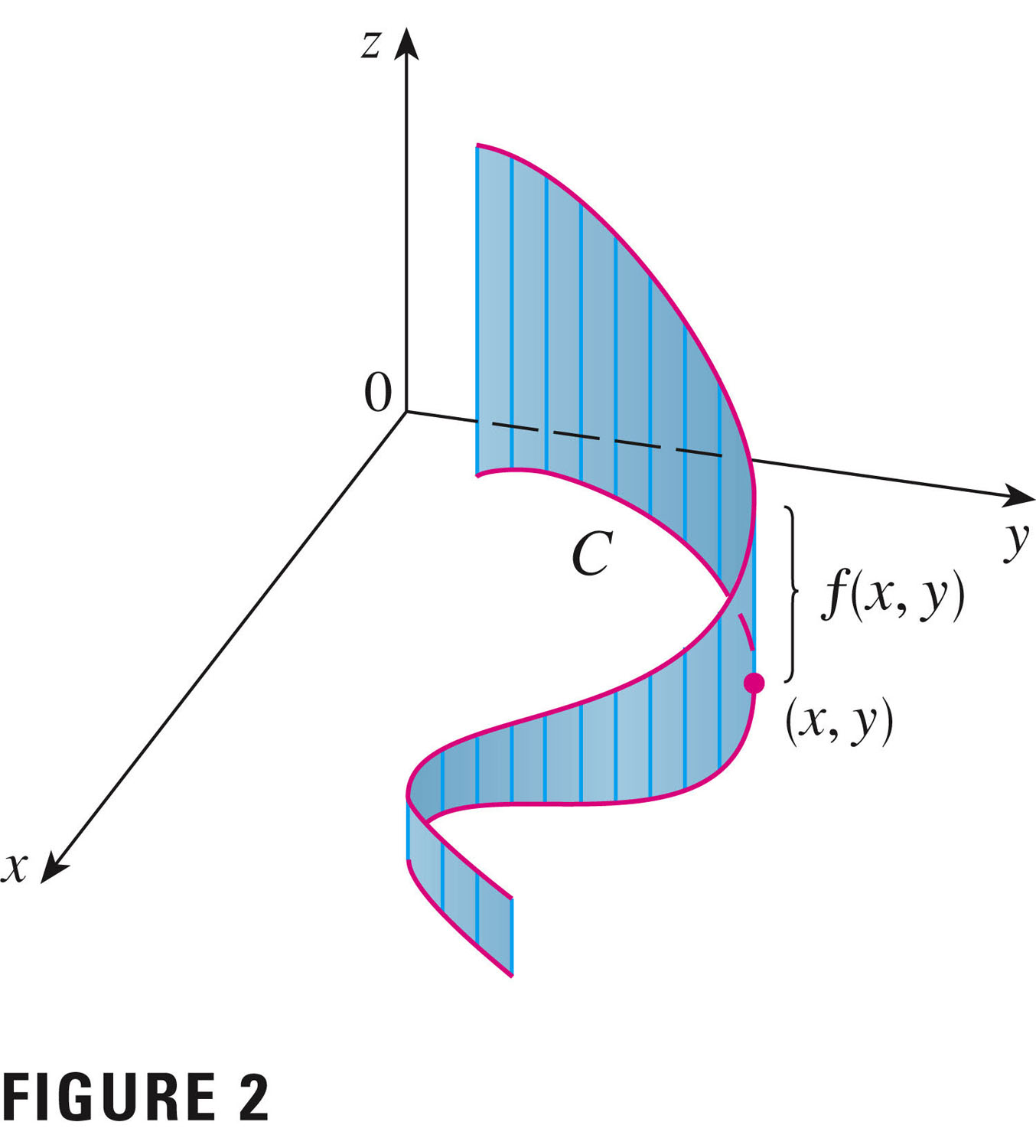
  Although with $f(x,y)=1$ we can also think of this as the length of the curve. Note: we think of $dt$ as positive (and it is, because we've specified the orientation). But if we reverse the orientation, we'd need to "reverse $dt$" as well.

• Rather than look at line integrals along the curve $C$, with differential $ds$, we could integrate components along the $x$ and $y$ directions: line integrals of $f$ along $C$ with respect to $x$ and $y$ are \[ \int_{C} f(x,y)dx = \int_{a}^{b} f(x(t),y(t)) x^{'}(t) dt \] and \[ \int_{C} f(x,y)dy = \int_{a}^{b} f(x(t),y(t)) y^{'}(t) dt \]
• Let's look at Example 4 first, then take on #8, p. 1096.

  Example 4, p. 1091

  • raises the issue of orientation -- in what sense is the curve traversed?
  • illustrates two different strategies of parameterization;
  • telegraphs a topic of section 16.3: path independence of line integrals.
  • We can think of re-think this one as a vector field problem.

• The vector parameterization of a line segment preceding Example 4 is a very useful trick:
  ${\bf{r}}(t)=(1-t){\bf{r}}_0+t{\bf{r}}_1\ \ 0 \le t \le 1$

  But it's not just vectors. We could parameterize points, for example. Or even images!

• Examples:
  • #8, p. 1096 (with lots of extra detail)
  • #12 (3-d versions of all of this is no big deal)

• Now we want to extend our line integrals to vector fields.

  Let ${\bf{F}}$ be a continuous vector field defined on a smooth curve $C$ traced out by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Then the line integral of ${\bf{F}}$ along $C$ is \[ \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot d{\bf{r}} = \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot {\bf{r}}^{'}(t) dt = \int_{C} {\bf{F}} \cdot {\bf{T}} ds \] where ${\bf{T}}$ is the tangent vector (the component of velocity in the direction tangential to the motion).

  If vector field ${\bf{F}}=P\hat{i}+Q\hat{j}+R\hat{k}$=$\langle P,Q,R \rangle$, then we can break the integral into three: \[ \int_{C} {\bf{F}} \cdot d{\bf{r}} = \int_{C} Pdx + Qdy + Rdz \] With my parentheses fascination, you can be sure that I'd like to put parentheses around that last integrand: $\int_{C} (Pdx + Qdy + Rdz)$ -- just to emphasize that the integration is over all....

  Examples:

  • #32
  • #52 is an interesting physics problem....

Wherein we discover the importance of gradient fields....

In this section there are certain definitions that we want to make note of:


Let $C$ be a smooth curve (note -- smooth!) given by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Let $f$ be a differentiable function of two or three variables whose gradient vector $\nabla f$ is continuous on $C$. Then \[ \int_{C} \nabla f \cdot d{\bf{r}} = f({\bf{r}}(b)) - f({\bf{r}}(a)) \]

Two nice ways to conceptualize that:

• Cartesian coordinates and differentials (p. 944)
• Parametrically (author's proof, p. 1100)

As the author mentions right after his proof, this is also true for piecewise smooth curves.

Examples:

• #1, p. 1106
• #3
  • By hook, or
  • By crook:

    Let ${\bf{F}} = P {\bf{i}} + Q {\bf{j}}$ be a vector field in an open, simply-connected region $D$. Suppose that $P$ and $Q$ have continuous first-order derivatives and \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \hspace{1in} \ throughout\ D \] Then ${\bf{F}}$ is conservative.

• Now let's have a look at the very important problem of the conservation of energy, p. 1105.

• Let's see why the "crook" works above. We'll do it via theorem 5, p. 1102:

  If ${\bf{F}}(x,y) = P(x,y) {\bf{i}} + Q(x,y) {\bf{j}}$ is a conservative vector field, where $P$ and $Q$ have continuous first-order partial derivatives on a domain $D$, then throughout $D$ we have \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \] This says that mixed partials of $f$ (essentially the potential of $ \bf{F}$) are equal -- the proof is Clairaut's theorem! $P=f_x$ and $Q=f_y$, and their partials are continuous (so the second partials of $f$ are continuous), so, by Clairaut's theorem, \[ f_{xy}=\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}=f_{yx} \]

• There are a couple of theorems that inform us about path independence, which we want to at least state. We've talked about path independence enough that you might be able to guess these by now:
  • The definition: \[ \int_{C} {\bf{F}} \cdot d{\bf{r}} \] is independent of path if \[ \int_{C_1} {\bf{F}} \cdot d{\bf{r}} = \int_{C_2} {\bf{F}} \cdot d{\bf{r}} \] for any two paths $C_1$ and $C_2$ in $D$ that have the same initial and terminal points.

  • Theorem: Suppose ${\bf{F}}$ is a vector field that is continuous on an open connected region $D$. If $\int_{C} {\bf{F}} \cdot d{\bf{r}}$ is independent of path in $D$, then ${\bf{F}}$ is a conservative vector field on $D$; that is, there exists a function $f$ such that $\nabla f = {\bf{F}}$.

  • The fundamental theorem tells us the converse of that: if ${\bf{F}}$ is a gradient (conservative) vector field continuous on an open connected region $D$, then it's path independent.
  Examples:
  • #11, p. 1106
  • #21
  • #35 -- assumptions matter! What's the domain of ${\bf{F}}$?