- Your 16.2 homework is due today.
- Your 16.3 homework is due Tuesday. That will be your last homework.
- Our last quiz will be at the end of the hour today.
Wherein we discover the importance of gradient fields....
-
In this section there are certain definitions that we want to make note
of:
- Cartesian coordinates and differentials (p. 944)
- Parametrically (author's proof, p. 1100)
- #1, p. 1106
- #3
- By hook, or
- By crook:
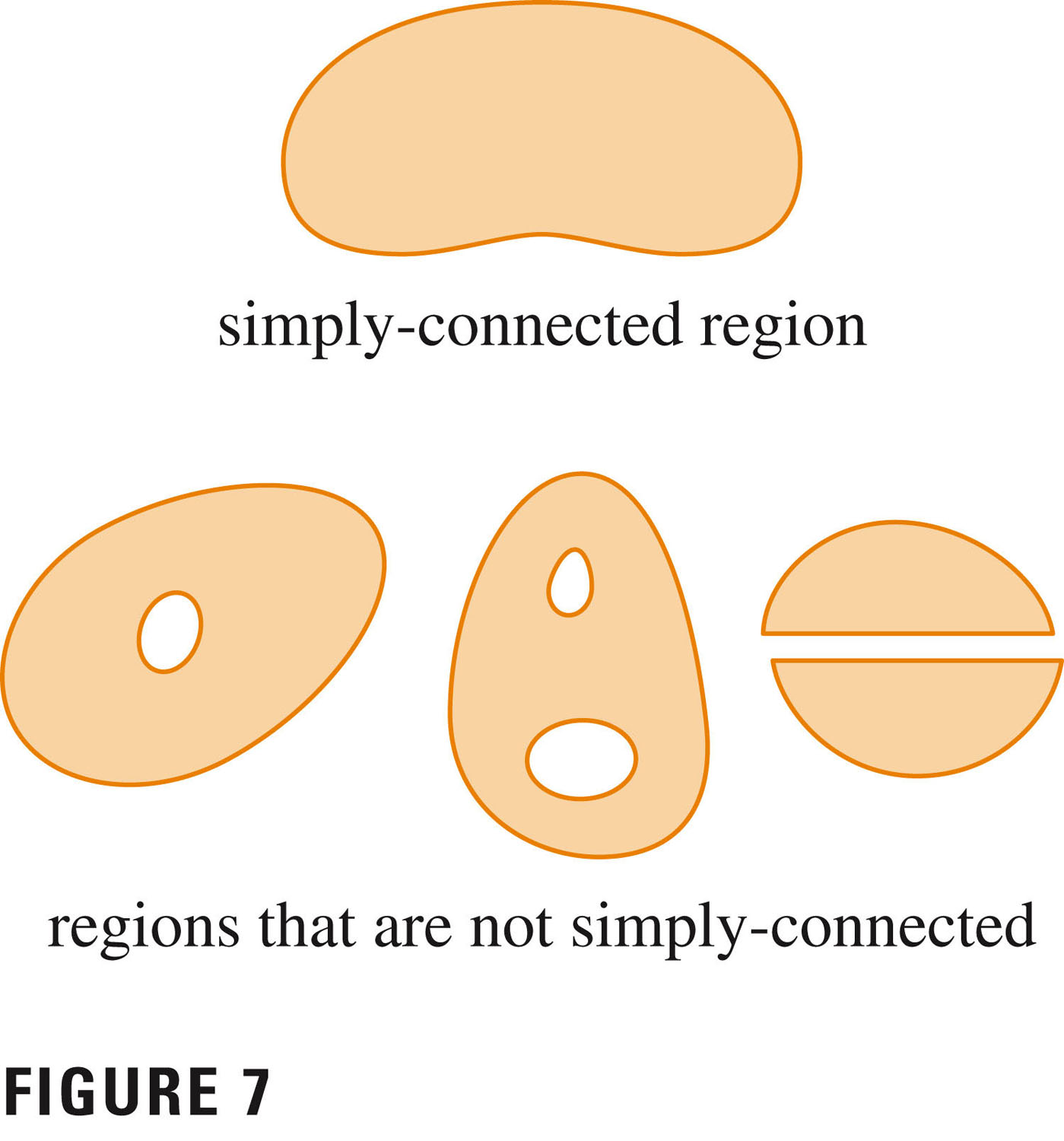
Let ${\bf{F}} = P {\bf{i}} + Q {\bf{j}}$ be a vector field in an open, simply-connected region $D$. Suppose that $P$ and $Q$ have continuous first-order derivatives and \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \hspace{1in} \ throughout\ D \] Then ${\bf{F}}$ is conservative (i.e., is a gradient field).
- Let's see why the "crook" works above. We'll do it via theorem 5,
p. 1102 (where we look at the converse):
If ${\bf{F}}(x,y) = P(x,y) {\bf{i}} + Q(x,y) {\bf{j}}$ is a conservative vector field, where $P$ and $Q$ have continuous first-order partial derivatives on a domain $D$, then throughout $D$ we have \[ \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} \] This says that mixed partials of $f$ (essentially the potential of $ \bf{F}$) are equal -- the proof is Clairaut's theorem! $P=f_x$ and $Q=f_y$, and their partials are continuous (so the second partials of $f$ are continuous), so, by Clairaut's theorem, \[ f_{xy}=\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}=f_{yx} \]
- There are a couple of theorems that inform us about path
independence, which we want to at least state. We've talked about
path independence enough that you might be able to guess these by now:
- The definition:
\[
\int_{C} {\bf{F}} \cdot d{\bf{r}}
\]
is independent of path if
\[
\int_{C_1} {\bf{F}} \cdot d{\bf{r}} = \int_{C_2} {\bf{F}} \cdot d{\bf{r}}
\]
for any two paths $C_1$ and $C_2$ in $D$ that have the same initial and
terminal points.
- Theorem: Suppose ${\bf{F}}$ is a vector field that is continuous
on an open connected region $D$. If $\int_{C} {\bf{F}} \cdot d{\bf{r}}$
is independent of path in $D$, then ${\bf{F}}$ is a conservative vector
field on $D$; that is, there exists a function $f$ such that $\nabla f
= {\bf{F}}$.
- The fundamental theorem tells us that the converse of that is also true: if ${\bf{F}}$ is a gradient (conservative) vector field continuous on an open connected region $D$, then it's path independent.
- The definition:
\[
\int_{C} {\bf{F}} \cdot d{\bf{r}}
\]
is independent of path if
\[
\int_{C_1} {\bf{F}} \cdot d{\bf{r}} = \int_{C_2} {\bf{F}} \cdot d{\bf{r}}
\]
for any two paths $C_1$ and $C_2$ in $D$ that have the same initial and
terminal points.
- Now let's have a look at the very important problem of the
conservation of energy, p. 1105.
Examples:
- #11, p. 1106
- #21
- #35 -- assumptions matter! What's the domain of ${\bf{F}}$?
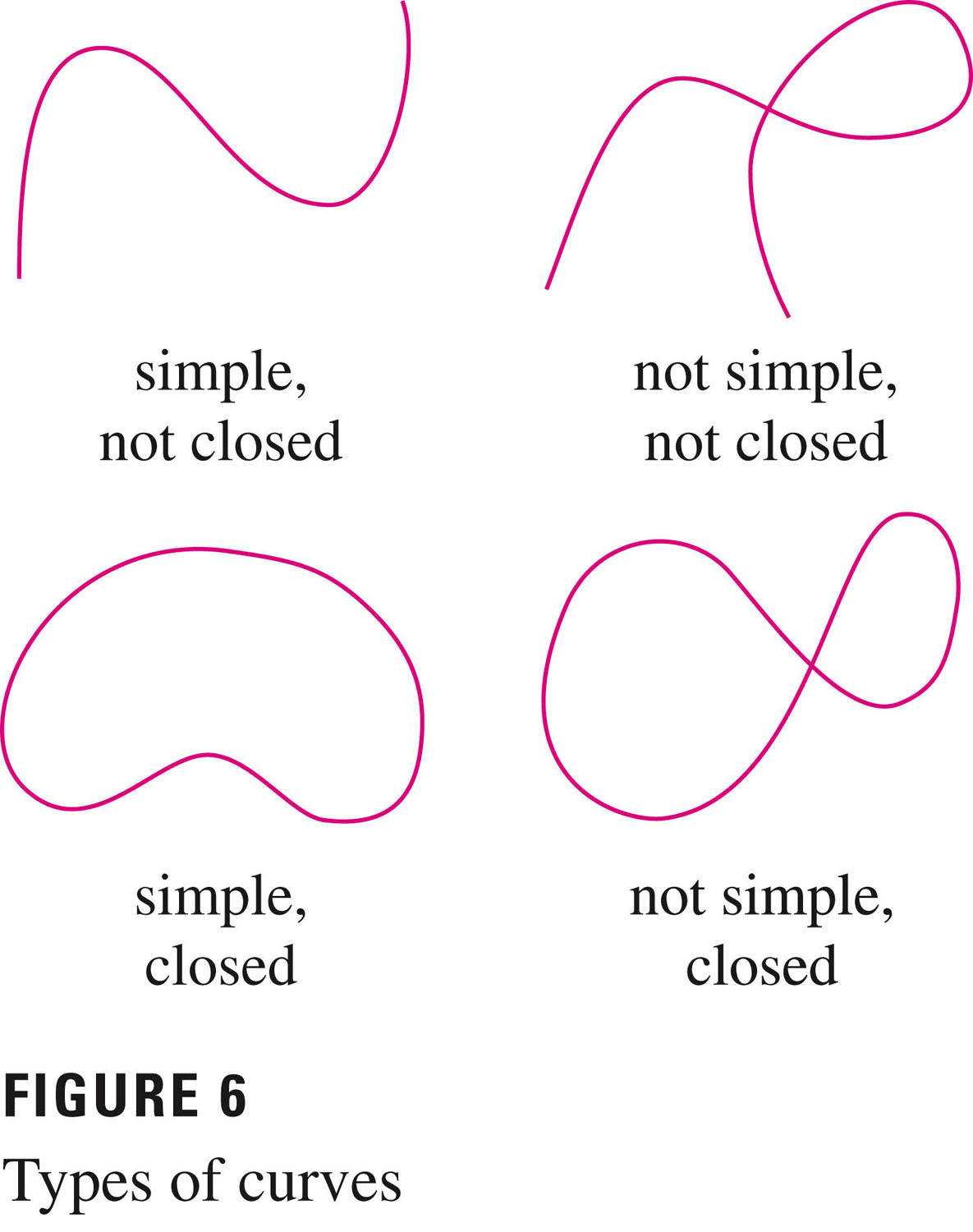
Let $C$ be a smooth curve (note -- smooth!) given by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Let $f$ be a differentiable function of two or three variables whose gradient vector $\nabla f$ is continuous on $C$. Then \[ \int_{C} \nabla f \cdot d{\bf{r}} = f({\bf{r}}(b)) - f({\bf{r}}(a)) \]
Two nice ways to conceptualize that:
As the author mentions right after his proof, this is also true for piecewise smooth curves.
Examples:
- Green's Theorem:
Let $C$ be a positively oriented, piecewise-smooth, simple closed curve in the plane and let $D$ be the region bounded by $C$ ($C$ is sometimes denoted $\partial D$ in this case, as the boundary of $D$). If $P$ and $Q$ have continuous partial derivatives on an open region that contains $D$, then \[ \oint_{\partial D} Pdx + Qdy = \int_{D}\int_{} \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA \]
Requiring an open region to contain $D$ means that the derivatives will exist on the boundary. That's why that's included.
- Let's look at the proof in the simple case of a Type I and II
region (#30).
- The reason that this theorem is useful is because sometimes the line
integral is easier, sometimes the area integral is easier -- so we can
choose to make our lives easier! Let's do....
Green's theorem is simply a calculation of a rather special integral on a two-dimensional region $D$: \[ \oint_{\partial D} {\bf{F}} \cdot d{\bf{r}} = \oint_{\partial D} Pdx + Qdy = \int_{D}\int_{} \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)dA \] It shows one way to handle the ``work problem'' $\int_{C} {\bf{F}} \cdot d{\bf{r}}$ when the field is not conservative. It can also be seen as a generalization of the Fundamental Theorem of Calculus to area integrals, in the sense that the integral defined on a region can be evaluated by considering only its boundary.
- Green's theorem can be used in a sneaky way to calculate areas with a
line integral: if we find functions $P$ and $Q$ so that
\[
A
=
\int_{D}\int_{}
dA
=
\int_{D}\int_{}
1
dA
=
\int_{D}\int_{}
\left(
\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}
\right)
dA
= \oint_{\partial D} Pdx + Qdy
\]
- Examples
- #30, p. 1115
- #1
- #3
- #19
- #22
- #23