- No quiz tomorrow. Just review.
- I will also plan a review session on Monday night, for anyone
who's interested. This will run from 7:00 to 8:30, while my son
is at Boy Scouts.
- Your 16.3 homework is returned: graded #4, 6, 20.
- I didn't grade 26 (or threw it out, actually), because you
struggled so mightily on the quiz!
- It appears plausible that 26 is a conservative vector field. It would be nice to find a potential function that gives rise to this. I'll give two GOHF cards to the first person who either produces that plot as a gradient field, or shows that it can't be conservative.
- #20: once you know that ${\bf{F}}$ is conservative, find
$f$ and use it! Don't do the line integral (unless it happens
to be easier than finding $f$....)
- Zach asked about #28.
- ${\bf{F}}(x,y)=\langle \cos(x - 2 y), -2 \cos(x - 2 y)\rangle$
- $\int {\bf{F}}\cdot {\bf{dr}} = 0$:
- $\int {\bf{F}}\cdot {\bf{dr}} = 1$:
- Note/hint: ${\bf{F}}$ is a gradient field.
- One more thing about #36.
- I didn't grade 26 (or threw it out, actually), because you
struggled so mightily on the quiz!
- Your last quiz is returned today:( Let's have a peek.
- How a planimeter works
- Two are on order! (Mine, and Aimee Krug's -- for the department)
- I'll hope to have it to show during the final. Maybe you'll be able to use it to do some of the problems on the final!:)
- Green's Theorem:
Let $C$ be a positively oriented, piecewise-smooth, simple closed curve in the plane and let $D$ be the region bounded by $C$ ($C$ is sometimes denoted $\partial D$ in this case, as the boundary of $D$). If $P$ and $Q$ have continuous partial derivatives on an open region that contains $D$, then \[ \oint_{\partial D} Pdx + Qdy = \int_{D}\int_{} \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA \]
Requiring an open region to contain $D$ means that the derivatives will exist on the boundary. That's why that's included.
- Let's look at the proof in the simple case of a Type I and II
region (#30).
- The reason that this theorem is useful is because sometimes the line
integral is easier, sometimes the area integral is easier -- so we can
choose to make our lives easier! Let's do....
Green's theorem is simply a calculation of a rather special integral on a two-dimensional region $D$: \[ \oint_{\partial D} {\bf{F}} \cdot d{\bf{r}} = \oint_{\partial D} Pdx + Qdy = \int_{D}\int_{} \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)dA \] It shows one way to handle the ``work problem'' $\int_{C} {\bf{F}} \cdot d{\bf{r}}$ when the field is not conservative. It can also be seen as a generalization of the Fundamental Theorem of Calculus to area integrals, in the sense that the integral defined on a region can be evaluated by considering only its boundary.
- Green's theorem can be used in a sneaky way to calculate areas with a
line integral: if we find functions $P$ and $Q$ so that
\[
A
=
\int_{D}\int_{}
dA
=
\int_{D}\int_{}
1
dA
=
\int_{D}\int_{}
\left(
\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}
\right)
dA
= \oint_{\partial D} Pdx + Qdy
\]
Today I want to show how the FTC can be deduced from Green's theorem, once again showing how many of the topics we have studied this semester are simple generalizations of ideas from univariate calculus.
- Examples
- #30, p. 1115
- #1
- #3
- #19
- #22
- #23
I wish that we'd had more time for this topic, and, in particular, for Maxwell's equations. It's one of the nice "applications" of multivariate calculus.
Curl and divergence rely on two vector products (cross and dot), and an understanding of operators (which may be unfamiliar).
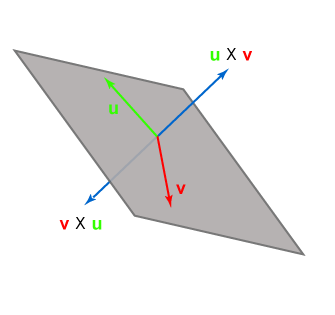
- Let's start with the cross-product:

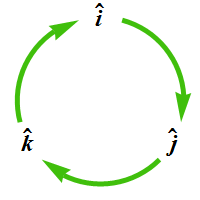

There are a few other properties of the cross-product that you should know:

- Let's begin getting serious by introducing the del operator:
\[
\nabla = \frac{\partial}{\partial x} {\bf{i}} +
\frac{\partial}{\partial y} {\bf{j}} +
\frac{\partial}{\partial z} {\bf{k}}
\]
We've seen $\nabla$ before, of course: when it acts on a scalar function $f$,
it returns the gradient of $f$, $ \nabla f$.
There are three ways that we use $ \nabla$:
- as an operator (which is a type of function, which takes functions as
arguments, rather than numbers). This is exemplified by the gradient, but also
by the Laplacian (described below).
Quoting again from Feynman (VII, p. 2-6): operators are, "...as Jeans said, 'hungry for something to differentiate.'"
- since we've represented del as a vector, we might use it to
multiply vector functions -- applying both of the two types of
vector multiplication (dot- and cross-products) -- and returning
functions.
- applied with the dot-product, $\nabla$ creates a scalar function;
- applied with the cross-product, $\nabla$ creates a vector function.
- as an operator (which is a type of function, which takes functions as
arguments, rather than numbers). This is exemplified by the gradient, but also
by the Laplacian (described below).
- Curl of vector field ${\bf{F}}=\langle P,Q,R \rangle$:
\[
{\textrm{curl}}{\ \bf{F}} =
\left(
\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}
\right)
{\bf{i}}
+
\left(
\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x}
\right)
{\bf{j}}
+
\left(
\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}
\right)
{\bf{k}}
\]
If curl ${\bf{F}} = {\bf{0}}$ at a point, then ${\bf{F}}$ is said to be
irrotational at that point:
Making use of $\nabla$, then, and the cross-product $\times$, we have
${\textrm{curl}}{\ \bf{F}} =\nabla \times {\bf{F}}$ We can use Green's theorem to try to understand the curl as rotation:
Start by switching to 2D (so F has no $z$-component). Then imagine a contour around a point, say a circle centered at the point, which is shrinking down to nothing. The picture is in your book, on page 1118 (without the shrinking part):
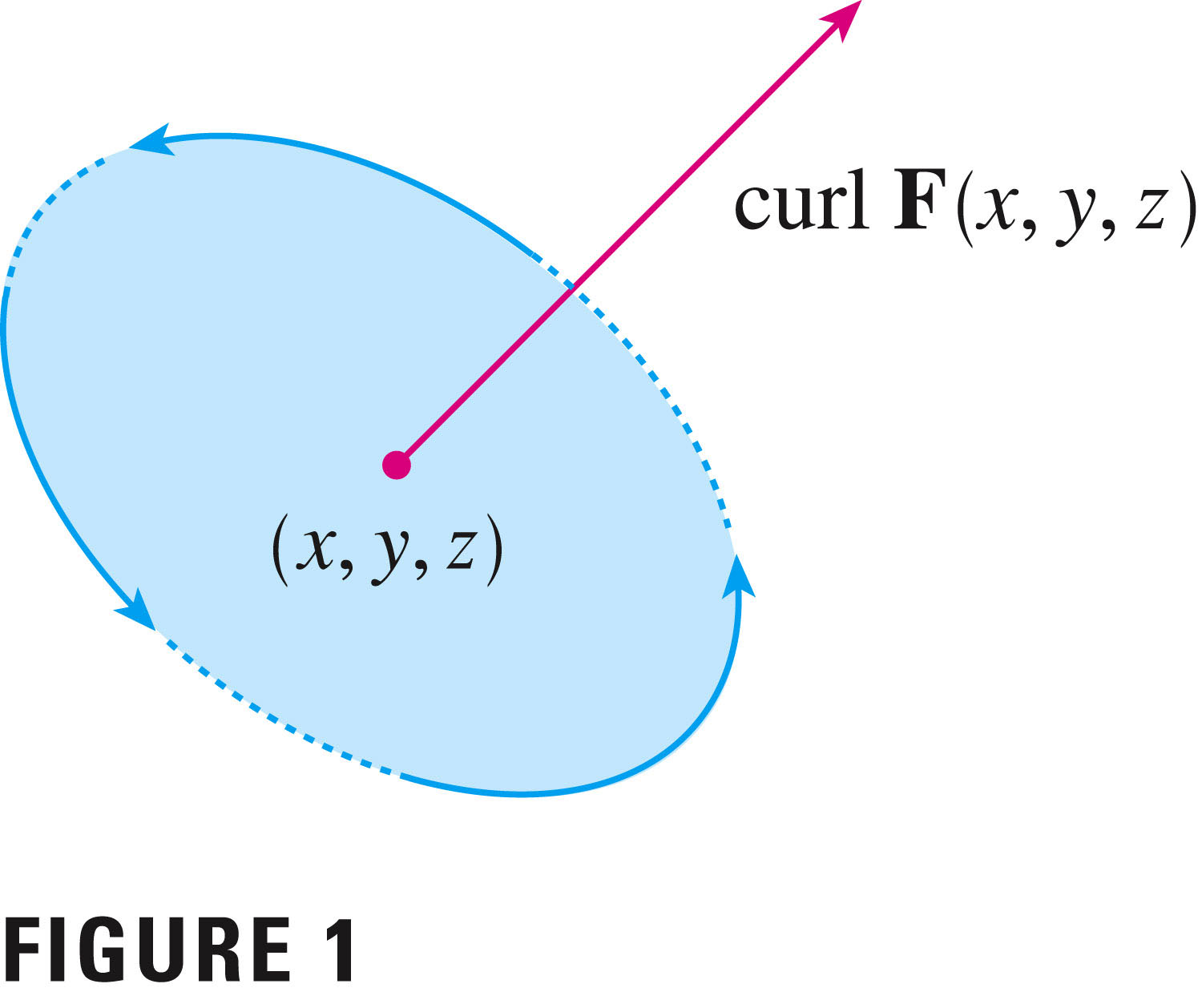
In the limit as the size of the circle shrinks to zero,
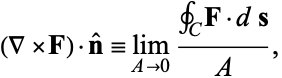
Q: What if $\bf{F}$ is conservative, i.e. a gradient field?
If $f$ is a function of three variables that has continuous second-order partial derivatives on disk $D$, then \[ {\textrm{curl}}(\ \nabla f) = {\textrm{curl}}\ {\bf{F}} = {\bf{0}} \] (note that that's a vector ${\bf{0}}$). This says that if ${\bf{F}}$ is conservative, then curl ${\bf{F}} = {\bf{0}}$.
This falls right out of the curl equations: \[ {\textrm{curl}}{\ \bf{F}} = \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) {\bf{i}} + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) {\bf{j}} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) {\bf{k}} \]
where $P=f_x$, $Q=f_y$, and $R=f_z$.
The proof is by Clairaut's theorem (generalized to 3D). Recall: Suppose $f$ is defined on a disk $D$ that contains the point $(a,b)$. If the functions $\frac{\partial^2 f}{\partial x \partial y}$ and $\frac{\partial^2 f}{\partial y \partial x}$ are both continuous on $D$, then \[ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} \]
The components of the curl are differences of mixed partials, as you've perhaps noticed. Hence, the curl of a gradient field is zero.
Theorem 4, p. 1117: If ${\bf{F}}$ is a vector field defined on all of $\Re^3$ whose component functions have continuous partial derivatives and ${\textrm{curl}}{\ \bf{F}} = {\bf{0}}$, then ${\bf{F}}$ is a conservative vector field.
Thus conservative vector fields are irrotational.
- Divergence:
\[
{\textrm{div}\ \bf{F}} =
\frac{\partial P}{\partial x} +
\frac{\partial Q}{\partial y} +
\frac{\partial R}{\partial z}
= \langle \frac{\partial }{\partial x},
\frac{\partial }{\partial y},
\frac{\partial }{\partial z} \rangle \langle P,Q,R \rangle
= \nabla \cdot {\bf{F}}
\]
Note that this is a scalar function, which measures the tendency of the vectors of $\bf{F}$ to flow out of (or into) a point.
If ${\textrm{div}\ \bf{F}} = 0$, then ${\bf{F}}$ is said to be incompressible.
Examples:
- #7, p. 1121
- #9-11
- The Laplacian operator is designated by $\nabla^2$, and creates a
scalar function from a scalar function. We can think of this as the dot
product -- a scalar -- of two vectors:
\[
\nabla^2 f = \nabla \cdot \nabla f
=
\frac{\partial^2 f}{\partial x^2}+
\frac{\partial^2 f }{\partial y^2}+
\frac{\partial^2 f }{\partial z^2}
\]
Solutions of Laplace's equation $\nabla^2 f = 0$ are called harmonic functions, and are very important in physics and complex analysis.
We can think of solutions of Laplace's equation as incompressible gradient fields: so fields that are simultaneously incompressible and irrotational.
- Examples: now that we've got all the machinary in place, let's
look at a couple of examples:
- #12, p. 1121
- #19: it turns out the $div\ curl{\bf{F}}=0$ -- p. 1119 -- again by Clairaut.
- #21: check curl
- #22: check div
- Maxwell's
equations should be the poster child for this section.
From the 11/22/2015 edition of the Guardian: Maxwell's equations: 150 years of light: "A century and a half ago, James Clerk Maxwell submitted a long paper to the Royal Society containing his famous equations. Inspired by Michael Faraday's experiments and insights, the equations unified electricity, magnetism and optics. Their far-reaching consequences for our civilisation, and our universe, are still being explored."
Light, electricity, and magnetism are brought together in these equations of physics.
Examples:
- #29 (we need this for #38)
- A rule for cross-products in general: ${\bf{A\times (B \times C)=B(A\cdot C)- (A\cdot B)C}}$
- #38 (Maxwell!)
- #37 (just to see curl in action)
- #29 (we need this for #38)