- Our first of two midterm exams is next week, and will cover
chapters 1-3 (the sections we've covered, at any rate). On
Monday we'll have a review. You'll be allowed a one-page (front
and back) sheet for the exam.
- Quiz today is over 3.2: recurrence relations
- There are student tutors at NKU who may be able to help:
- Learning Plus: Mitch Playforth
- Of those in the Math/Stat lab (MP457), Sydney, Nghia and William are all CS majors so they may be able to help. Here are their hours.
- We analyzed two algorithms: binary search, and the Euclidean algorithm.
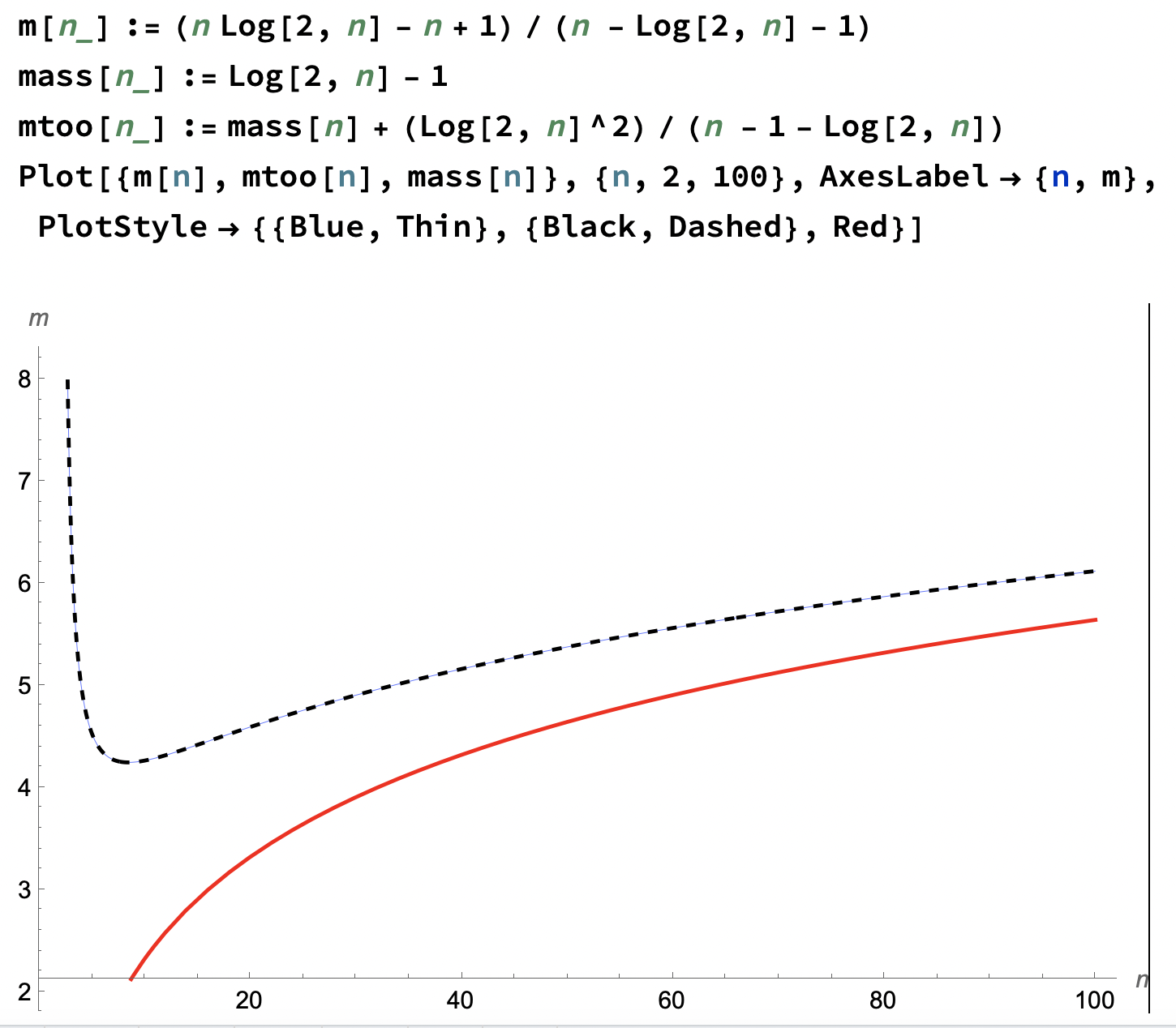
- Binary search: requires a sorted list, so we added a mergesort first, which was fairly expensive:
\[
n \log_2(n)-n+1
\]
If one is doing a one-off search, then use sequentialsearch -- requiring \(n\) comparisons in the worst case. But if one is doing multiple searches of the list, then it may pay to sort it first:
- Euclid's GCD (Greatest Common Divisor)
has a ratio of Fibonacci numbers as the worst case, which we discovered with this handout.
- Binary search: requires a sorted list, so we added a mergesort first, which was fairly expensive:
\[
n \log_2(n)-n+1
\]
- Marked up
- We'll finish off 3.3: Analysis
of Algorithms,
- with a quick example illustrating a linear, first-order, non-constant coefficient recurrence relation (#12, p. 196): \[ \begin{array}{ll} {S(1)=2}&{}\cr {S(n)=3(n+1)S(n-1)}&{n \ge 2} \end{array} \]
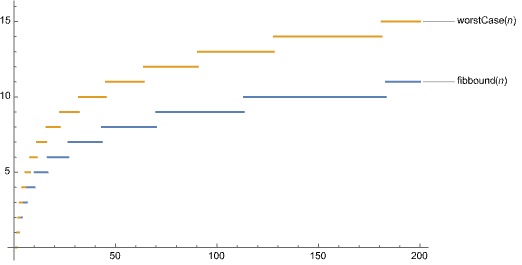
- a wrap-up of Euclid's GCD (Greatest Common Divisor), whose
upper bound calculation will lead us to a
divide-and-conquer recurrence, with worst case
\[
E(n) \le 2\log_2(n).
\]
Last time we used this handout to discover that the worst-case scenario is successive Fibonacci numbers, e.g. \[ gcd(89,55) \] Using the fact that \[ F(n) = \text{Round}\left(\frac{\phi^n}{\sqrt(5}\right) \] for all \(n \ge 1\), we can get a tighter bound on \(E(n)\): \[ E(n) \le \text{Round}\left[\log _{\phi }\left(\sqrt{5} a\right)\right]-2 \] where \(\phi\) is the golden mean or ratio: \[ \phi = \frac{1+\sqrt{5}}{2} \]
- We'll get a start on Section 4.1
(Sets).
- Then have a quiz....