Traversing a Binary Tree
|
Traversing a binary tree comes in handy when you would like to do a print out
of all the data elements in the tree. We demonstrate three types of traversals in our
tutorial.
All traversal descriptions refer to:
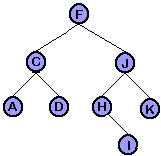 Figure 1.1: Sorted Binary Tree These three types are as follows:
|
Pre order traversal:A pre order traversal prints the contents of a sorted tree, in pre order. In other words, the contents of the root node are printed first, followed by left subtree and finally the right subtree. So in Figure 1.1, a pre order traversal would result in the following string: FCADJHIK. |
PreOrder (T)
If T < > Null
then print (T.data)
else print(‘empty tree’)
If T.lp < > null
then PreOrder(T.lp)
If T.rp < > null
then preorder (T.rp)
end.
|
|
In order traversal:An in order traversal prints the contents of a sorted tree, in order. In other words, the lowest in value first, and then increasing in value as it traverses the tree. The order of a traversal would be 'a' to 'z' if the tree uses strings or characters, and would be increasing numerically from 0 if the tree contains numerical values. So in Figure 1.1, an in order traversal would result in the following string: ACDFHIJK. |
InOrder (T)
If T < > null
print (‘empty tree’)
If T.lp < > null
then InOrder(T.lp)
print (T.data)
If T.rp < > null
then InOrder (T.lp)
end.
|
|
Post order traversal:A post order traversal prints the contents of a sorted tree, in post order. In other words, the contents of the left subtree are printed first, followed by right subtree and finally the root node. So in Figure 1.1, a post order traversal would result in the following string: ADCIHKJF. |
PostOrder (T)
If T = null
then print (‘empty tree’)
If T.lp < > null
then PostOrder(T.lp)
If T.rp < > null
then PostOrder(T.lp)
Print(T.data)
end.
|
|
|
If the word right is replaced by left and vice versa in the above definitions the result is called the Converse of the definition. (I.e. ConversePreOrder – Process the root, the right subtree and then the left subtree) |