Kriging is based on the Variogram

Here's a one-dimensional example:

Formally, the weights of the estimation scheme are determined as follows:

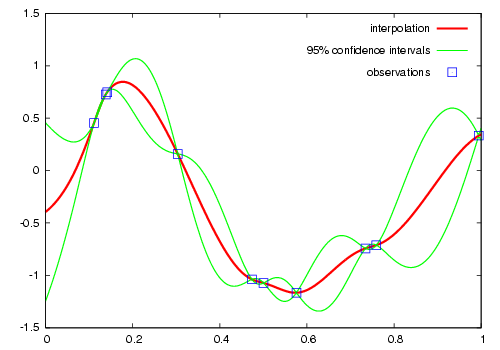
$ \left[ \begin{array}{c} \lambda_1 \\ \vdots \\ \lambda_n \\ \mu \end{array} \right] = \left[ \begin{array}{cccc} \gamma(x_1,x_1) & \cdots & \gamma(x_1,x_n) &1 \\ \vdots & \ddots & \vdots & \vdots \\ \gamma(x_n,x_1) & \cdots & \gamma(x_n,x_n) & 1 \\ 1 &\cdots& 1 & 0 \end{array} \right]^{-1}\,\, \left[ \begin{array}{c} \gamma(x_1,x^*) \\ \vdots \\ \gamma(x_n,x^*) \\ 1 \end{array} \right] $

Then the interpolation by ordinary kriging is given by:

$ \hat{Z}(x^*)= \left[\begin{array}{c} z_1 \\ \vdots \\ z_n \\ 0 \end{array} \right]^T \,\, \left[\begin{array}{cccc}\gamma(x_1,x_1) & \cdots & \gamma(x_1,x_n) &1 \\ \vdots & \ddots & \vdots & \vdots \\ \gamma(x_n,x_1) & \cdots & \gamma(x_n,x_n) & 1 \\ 1 &\cdots& 1 & 0 \end{array} \right]^{-1}\,\, \left[\begin{array}{c}\gamma(x_1,x^*) \\ \vdots \\ \gamma(x_n,x^*) \\ 1\end{array}\right] $