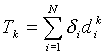
A case-control test for spatial clustering that accounts for geographic variation in population density.

Data Requirements

spatial locations of cases and controls

Analysis

H₀: cases and controls are sampled from a common spatial point distribution

H_a: the cases are spatially clustered relative to the controls

Test Statistic: The test statistic is the sum, over all cases, of the number of each case’s k nearest neighbors that also are cases. Define d _i = 1 if observation i is a case and 0 if it is a control;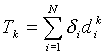

if the k^th nearest neighbor to i is a case and 0 otherwise. The test statistic is

The expected value of the test statistic under the null hypothesis is

where N is the sample population size and

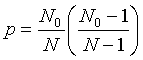
where N₀ is the number of cases.

The variance is a fairly complex expression and is given in Cuzick and Edwards (1990). It can be used to calculate a z-score which is distributed as a normal deviate and can be used to evaluate significance.

When cases are clustered the nearest neighbor to a case will tend to be another case, and the test statistic will be large.

Output

Results table

first column is k, the number of nearest neighbors
second column is T_k, the test statistic
third column is E[T_k], the expected value of T_k under H₀
forth column is the variance of T_k under the null
fifth column is the z-score
sixth column is the probability under H₀, of observing T_k as large or larger than the one given in column 2

The p-values from each row are combined using both the Bonferroni and Simes corrections

Upper and lower bounds on T_k are calculated when distance ties are encountered (Jacquez, 1994)

Map case and control locations

arrows indicate first nearest neighbor links between cases
arrow head identify the nearest neighbor and the arrow tails the case being evaluated
two-headed arrows indicate reflexive nearest neighbors

References

Cuzick, J. and Edwards, R. 1990. Spatial clustering for inhomogeneous populations. Journal of the Royal Statistical Society Series B, 52:73-104.

Jacquez, G.M. 1994. Cuzick and Edwards’ test when exact locations are unknown. American Journal of Epidemiology, 140:58-64.

Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.