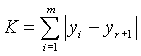
A test for temporal clustering in one or more time series. It is sensitive to single clusters such that cases occur at about the same time, and measures the dispersion of cases about a central time period. Currently the software provides two tests for temporal clustering; within the individual spatial units and across all spatial units simultaneously.

Data Requirements

Counts of cases in consecutive time intervals

rare data are required because at least one time interval must have 0 cases, at the same time two or more of the time intervals must have cases
normality assumption used to evaluate significance doesn’t hold when the time series is shorter than 10 intervals
cannot use rates, counts are required, therefore the method is biased by changes in population size through time

Analysis

H₀: cases occur randomly through time

H_a: cases cluster about a single point in time

Test Statistic: The test statistic K, measures the tendency of time periods with at least one case to form a single cluster in time: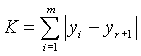

Where m is the number of time periods with at least one case, y_i is the time assigned to the i^th cell in which a case occurred. The index (r+1) is the ‘central most’ time cell that contained a case (). K will be small when cases form a single time cluster.

The expectation and variance of K under the null hypothesis are:

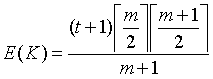
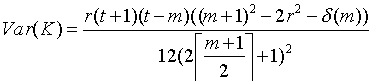
Where delta(m) = r-2 when m is odd, and delta(m) = 2r-1 when m is even. The test statistic K can be expressed as a z-score which is expected, under the null hypothesis of a random allocation of occupied cells across the time series, to be normally distributed with a mean of 0 and unit variance:

A z-score of 0 is consistent with a random allocation of occupied cells across the time series. K will be smaller than its expectation when occupied time intervals form a unimodal cluster, and the z-score will be less than 0. A uniform distribution of occupied time intervals through time will cause K to be larger than its expectation, and the z-score will be greater than 0. K will also be large when occupied time intervals form several clusters, and Larsen’s method thus cannot distinguish a uniform distribution from multiple clusters. Significance is therefore evaluated as a one-tailed test describing the probability, under the null hypothesis, of obtaining a K as small or smaller than the observed. This p-value is obtained by comparing the z-score to the percentiles of the normal distribution.

When the data consist of several time series the K statistics from each time series can be combined into an overall z-score as

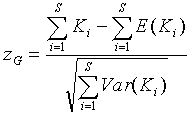
This grand z-score tests for an overall departure from the expected values across all time series simultaneously. The individual z-scores test for unimodal clustering within each time series. You must examine the individual z-scores before concluding whether a significant grand z-score is due to unimodal clustering in all of the time series, or to some other combination of temporal pattern across time series.

Output

For each time series:

K, and its expectation E(K) and variance Var(K)
z score and its one-tailed p-value

Plot K on its expectation (E(K))

each time series is one point on the graph
dashed line of the function K=E(K) describing where observations would be plotted under the null hypothesis of a random distribution of occupied intervals across the time series

Reference

Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.