Mantel's Test Example
Mantel method
�
Description: Mantel (1967) circumvented problems associated with
selecting the critical distances for the Knox test by first calculating time
and space distance matrices. His test statistic is the sum, across all case
pairs, of the time distance multiplied by the spatial distance.
�
Notation:
Ø
N : Number of cases
Ø
tij: Distance between cases i and j in time
Ø
sij : Distance between cases i and j in space
Ø
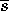 ,
,
 : Average space and time distances
: Average space and time distances
Ø
ss, st : Standard deviations of the space & time distances
Ø
Z : Test statistic, also called the Mantel product,
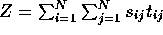
Ø
r : Standardized Mantel statistic,
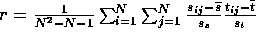
�
Null hypothesis: The time distances are independent of the space distances.
�
Significance: Although Mantel provides an approximation for the variance of Z under the null hypothesis of no association between space and time, the usual approach is to generate the distribution of Z using a Monte Carlo method, permuting the elements of one of the distance matrices while holding the other constant. This is equivalent to repeatedly scrambling the time observations across the localities, and calculating Z each time. This is done `Number of runs' times to generate a distribution of Z under the null hypothesis. A P-value is obtained by comparing the test statistic to this null distribution. Let NGE by the number of times Z under simulation was greater than or equal to Z (the observed test statistic) obtained from the original data. Nruns is the number of simulations. The P-value is then

�
Data screen: Select `Space-time' from the horizontal method menu, `Mantel' and `Data'. You need to specify the space and time distance matrices, whether to transform the distances, the kind of transformation to use, the constants to use for the data transformation and the number of runs to use when evaluating statistical significance. The distance matrices are generated by the distance module (see `Distance methods', in this Chapter). Enter `Epidemic.geo' and `Epidemic.tmp' for `Distance file 1: ' and `Distance file 2:'. Set `Number of runs : ' to 249. For a contagious disease we expect the small space and time distances to be correlated, but not the large distances. Mantel therefore recommended the use of the reciprocal transformation (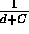 ) to reduce the effect of large space and time distances. Here C is a constant and d is the distance to be transformed. Be sure to enter a constant when you choose transformations that require a constant. The selection of a transformation and constant is subjective, and for this example let's use the raw distances. Stat's available transformations are:
) to reduce the effect of large space and time distances. Here C is a constant and d is the distance to be transformed. Be sure to enter a constant when you choose transformations that require a constant. The selection of a transformation and constant is subjective, and for this example let's use the raw distances. Stat's available transformations are:
Ø
None
Ø
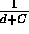
Ø
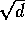
Ø
d2
Ø
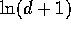
Run Screen: Press `F10' to exit, then select `Run' to begin calculations. The Mantel run screen will be displayed and the 249 simulations you requested will begin. The window on the right is a scattergram of the time distances on the space distances. Association between time and space distances appear as patterns in the scattergram. The points will form a line with positive slope when there is perfect correlation between the space and time distances. The points are scattered throughout the plot, with perhaps a hint of a denser accumulation of points for smaller space and time distances.
�
The frequency distribution of r under the null hypothesis is displayed in the window on the left. The standardized test statistic, r, is shown by the vertical line. It also is printed in the top window (Mantel r : 0.15405), which includes file names (Epidemic.geo, Epidemic.tmp), data transformation (None), number of runs (249) and the number of cases (30).

�
Significance is evaluated through an approximate randomization that shuffles the rows and columns of one distance matrix while holding the other distance matrix constant. Mantel's cross-product is calculated for every randomization, and a distribution of the Mantel statistic results. r for these data is just to the right of the distribution and is significant (P=0.0240), suggesting a positive association between the space and time distances. We used Nruns=249 to generate the null distribution, which means the smallest P value we can resolve is
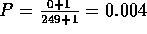 . We conclude there is significant interaction.
. We conclude there is significant interaction.
�
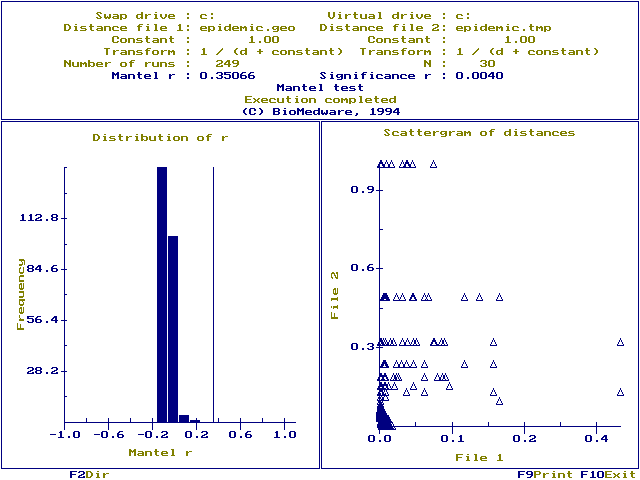
These data (epidemic.pnt) were generated using a contagious process. Six parent cases were distributed at random through space and time, and then spawned daughter cases that clustered about them. This gives rise to interaction since small geographic distances will be correlated with small time distances. Notice, however, the relationship between the space and time distances is non-linear, because small distances are correlated while larger ones are not. Would the reciprocal transformation help? Return to the data entry screen and change `Constant' to `1' and `Transform' to `1/(d+constant)' for both `Distance file 1' and `Distance file 2 '. Then run Mantel's method again.
�
The scattergram of the transformed distances is far more linear, and Mantel's r has increased to 0.35066 and is highly significant (P=0.0040). The reciprocal transformation increased the sensitivity of Mantel's method.
�
Notes: r is a measure of matrix correlation with range from -1 to 1. It is easier to interpret than Mantel's Z. Both r and Z become large when the time distances are linearly dependent on the space distances. A non-linear dependence of time on space therefore will not necessarily result in a significant Mantel test. Contagion is expected to cause small temporal and spatial distances to be correlated, while intermediate and large distances will be independent. The Mantel test is not sensitive under this arrangement of distances. One can use transformations (such as 1/(d+C), where C is a constant and D is the distance) to reduce the influence of larger distances, but the selection of the transformation is somewhat subjective.
Website maintained by Andy Long.
Comments appreciated.
![]()
![]()


