Mantel’s method

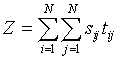
A test for space-time interaction using space and time distances.

Space and time distances between cases

• can specify distance transformation functions
• for a contagious disease we expect the small space and time distances to be correlated and Mantel recommended the use of a reciprocal transformation

Number of replicate runs to determine the null distribution of the test statistic

H₀: spatial distance between cases is independent of the time distance between those cases

H_a: nearby cases tend to occur at about the same time

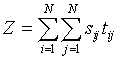
Where N is the number of cases, t_ij is the distance between cases i and j in time, and s_ij is the distance between cases i and j in space. When space-time interaction is present cases near in space will also be near in time, and the test statistic will be large if the reciprocal transformation is applied to the distances.

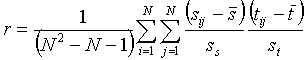
Where are average space and time distances and s_s and s_t are standard deviations of the space and time distances. r is a measure of matrix correlation with range –1<r<1.

Both r and Z become large when the time distances are linearly dependent on the space distances. A non-linear dependence of time on space therefore will not necessarily result in a significant Mantel test.

The usual approach to determining the significance of Mantel’s test statistic under H₀ is to use a Monte Carlo method, permuting the elements of one of the distance matrices while holding the other constant. This is equivalent to repeatedly scrambling the time observations across the localities, and calculating Z each time.

Mantel’s r and its significance

Scatterplot of time distances on space distances

• association between time and space distances appear as patterns in the scattergram

A frequency distribution of r under H₀ is plotted

Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.