More about Moran's I

Moran's I method

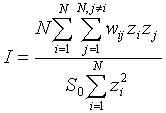
A test for spatial autocorrelation in disease rates. Positive spatial autocorrelation means that nearby areas have similar rates, indicating spatial clustering.

Let's think of the areas as counties (although they could be any geographic unit). Data Requirements

Disease rates linked to connection weights for locality pairs

weights are usually based on geographic adjacency or distance

The rule of thumb is to use a weighting scheme that reflects the alternative hypothesis.

each row in the weight file indicates the county under consideration, the value of the weight to be assigned, the number of counties that are to be connected to the county under consideration, and a list of the connected counties
only record non-zero weights
the weights are stored in a symmetric matrix, such that the weights are reflexive

Number of Monte Carlo runs to perform

Analysis

H₀: disease rates are spatially independent and assigned at random among the regions

H_a: disease rates are not spatially independent

Test Statistic: Moran's I is a weighted product-moment correlation coefficient, where the weights reflect geographic proximity. Values of I larger than 0 indicate positive spatial autocorrelation; values smaller than 0 indicate negative spatial autocorrelation.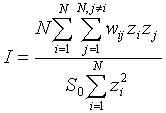

where N equals the number of regions, w_ij is a weight denoting the strength of the connection between areas i and j, z_i is the rate in region i centered about the mean rate (using z_i = x_i - ave(x); x_i is the rate in region i); and S_o is the sum of the weights, 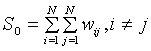. The weights reflect how "connected" we think two areas are, and usually reflect geographic proximity. Moran's I is used to determine whether "connected" areas are more similar to one another than would be expected under spatial randomness. It asks: Do the rates in connected areas covary? Nearby areas tend to have similar rates when their populations and exposures are alike. When rates in connected (nearby) areas are similar Moran's I will be large and positive. When rates in connected areas are dissimilar Moran's I will be negative.

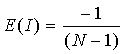
The expectation of I under the null hypothesis is:

The expectation becomes close to 0 as N increases. The variance of I is determined under two null hypotheses or assumptions: Normality (denoted N) or randomization (denoted R). Under assumption N the rates are sampled from a population whose distribution is normal. Under assumption R the rates are random samples from a population whose distribution is unknown. Assumption N is useful when we have good reason to believe the observations follow a normal distribution. Assumption R is less restrictive and, since we often don't know their theoretical distribution, is appropriate for disease rates. The variance under assumption N is:

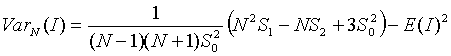
Under the assumption R the variance is:

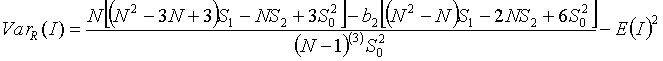
where a falling factorial is written s^(b)=s(s-1)...(s-b+1),

and where

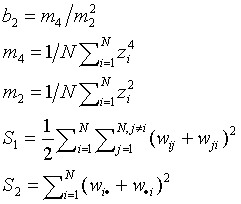
The significance of Moran's I is evaluated under assumptions R and N, and also by Monte Carlo simulation. For assumptions N and R z-scores are expressed as the difference between the observed and expected value of I in standard deviation units.

Output

P-values

two-tailed p-value because spatial pattern is of interest both when Moran's I is positive or negative

when the number of regions is greater than 25 the p-value obtained for assumption R closely approximates the p-value under Monte Carlo simulation

Plot of Moran's I under simulation

Reference

Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.