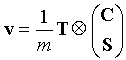
The direction method is a test for space-time interaction and is also used to determine the average direction of advance of a spread of cases. The method is sensitive to a systematic, directional spread of cases. This pattern occurs when an epidemic sweeps through an area. It also arises from geographically localized exposures, with individuals near the source receiving higher doses and showing symptoms before those further from the source. The term ‘chain of infection’ will be used to describe the sequence of occurrence of cases, it does not imply that the sequence of cases was the result of an infectious disease. You cannot infer a directional process from the direction test, you can, however, determine whether the observed spread of cases tends to be in one direction.

Data Requirements

Spatial locations of cases and controls

Way in which cases are ‘connected’ to create vectors as a directed time measure

Number of replicate runs to determine the null distribution of the test statistic

Analysis

H₀: No association between the times at which cases occur and the directions of the vectors formed by connecting the spatial locations of each case.

H_a: The direction from one case to the next is similar for cases that occur about the same time

Test Statistic: A chain of infection is constructed by first sequencing the cases by time of occurrence. The earliest case would be first, followed by the second case and so on. An arrow is then drawn from the location of the first case to the location of the second case, and this is repeated until all cases are connected. The chain of infection has at least two ends (the first and last cases), and branches when cases occur at exactly the same time. The test statistic is a vector whose direction is the average direction of the arrow comprising the chain of infection, and whose magnitude is the angular variance of those arrows: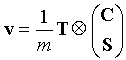

where C is a cosine matrix whose elements are c_ij,

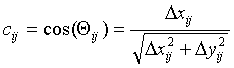
S is a sine matrix whose elements are s_ij,

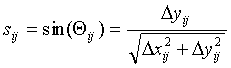
T is a time connection matrix describing the proximity, in time, of the cases to one another.

(x_i, y_i) are the geographic coordinates of case i, Dx_ij is the distance on the x axis between cases i and j (x_i-x_j), Dy_ij is the distance on the y axis between cases i and j (y_i-y_j), and Q_ij is the angle between a horizontal line and the vector connecting cases i and j.

The elements of the time connection matrix are determined by the researcher to reflect the suspected temporal scale of the pattern in N cases that occurred at times (t₁,…,t_N). The relative directed time measure, where t_ij = 1 if t_j>t_i, 0 if t_j=t_i, and –1 if t_j<t_i, used when all vectors connecting each case to all of the cases that follow it should be included. This is appropriate when it is hypothesized that a directional process operates on a longer time span, and cases that may be several links removed in the chain of infection are to be connected. The adjacent directed time measure, where t_ij = 1 if t_j is just after t_i, -1 if t_j is just before t_i, and 0 otherwise, is used when each case should only be connected to its temporal nearest neighbors. These are the cases that occur just before and just after the case, and is appropriate when it is hypothesized that there are directional effects of short duration. The following directed time measure, where t_ij = 1 if t_j is just after t_i and 0 otherwise, is used when each case should only be connected to the case (or cases) that immediately follow it. This is appropriate when tracing the average direction of the chain of infection.

The vector v points in the average direction of advance of the spread of cases, and its magnitude (termed the angular concentration) represents the variance in the angles between connected cases. When the magnitude is small the variance in the angles is large, and when the magnitude is large the variance in the angles is small. Angles are taken as counter clockwise degrees from horizontal, with East corresponding to 0 and North to 90. Concentration is in the range of 0 to 1, with 1 indicating an angular variance of 0. A consistent direction of spread of cases will result in an angular concentration near 1. A random spread of cases will result in an angular concentration near 0.

When the arrows all point in the same directions the angular variance is small, and when they point in many directions the angular variance is large. When directional components exist the chain of infection from one case to the next will proceed in common direction, and the test will be significant because the concentration will be small.

The significance of the average direction is evaluated through a randomization procedure which holds the sine and cosine matrices constant and randomly assigns connections between pairs of cases. This is equivalent to holding the locations of the cases fixed while randomizing their times of occurrence. This randomization is repeated to generate a distribution of the angular concentration under H₀. A p-value is determined by comparing the angular concentration from the original (not randomized) data to this null distribution.

Output

Results table

average angle
angular concentration
significance

Plot of frequency distribution of the angular concentration

Map of chain of infection

the average angle is shown on the map as a vector with the first case at its tail, and pointing in the average direction of advance

Reference

Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.