- when 2 cases are in the same area the weight assigned is wii=2/di
- weights for 2 different areas, i and j, are set to wij unless otherwise specified
- weights read from the connection file are divided by
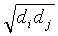
Moran’s I adjusted for population size
A test for spatial autocorrelation in disease rates that accounts for geographic variation in population size.
Data Requirements
Population sizes and disease rates
Link file with connection weights, rules are as follows:
Number of Monte Carlo runs
Analysis
H0: probability of a case occurring in an area is given by the proportion of the total population in that area, or in other words, the geographic variation in the number of cases is expected to follow geographic variation in population size
Ha: geographic variation in the number of cases does not follow geographic variation in population size
Test Statistic: Ipop is a spatial autocorrelation coefficient adjusted for the size of the population at risk.
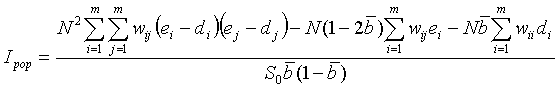
where m is the number of regions, N is the total number of cases in all of the regions, ni is the number of cases in area i, i is the proportion of cases in area i (ei = ni/N), X is the total size of the risk population in all of the areas, xi is the size of the risk population in area i, di is the proportion of the population in area i (di = xi/X), ei – di is the difference between the proportion of cases in area i and the number of cases expected given the areas population size, wij is the weight for areas i and j (the weights describe the alternative spatial model defining how ‘connected’ the areas are), and:
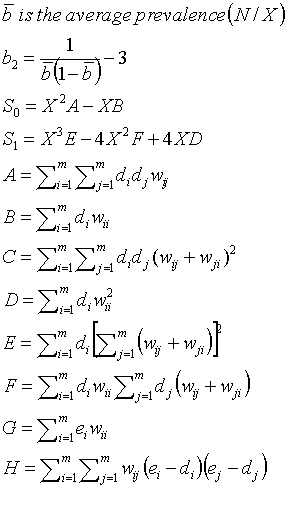
Large values of Ipop indicate positive spatial autocorrelation or similar rates in connected areas; small values indicate negative spatial autocorrelation or dissimilar rates in connected areas. Ipop is large under two clustering scenarios, first, when cases cluster within counties (because ei – di becomes large) and second, when regions with may cases are adjacent. The range of Ipop depends on population size, and it is useful the standardize the statistic using:
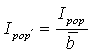
Expectation of Ipop under H0 is:
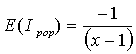
The variance of Ipop under H0 is:
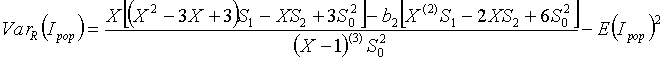
An approximation can also be calculated for the variance:
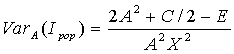
Significance is evaluated using three approaches: by Monte Carlo simulation, under the randomization assumption and by approximation. Under simulation the cases are allocated at random among the regions according to the proportion of the total population in each region. Under the randomization assumption a z-score can be calculated as the difference between the observed and expected value of Ipop in standard deviation units. A two-tailed p-value is reported because spatial pattern is of interest both when Ipop is positive or negative.
Ipop, Ipop’, E[Ipop]
Variance and significance under randomization assumption, approximation, and simulation
Plot of frequency distribution of Ipop obtained under simulation
Reference
Jacquez, G.M. 1994, User manual for Stat!: Statistical software for the clustering of health events, BioMedware, Ann Arbor, MI.