K-nearest neighbor method

This method is used to detect space-time interaction.

Data Requirements

Space and time distances between pairs of cases

Number of replicate runs to determine the null distribution of the test statistic

Analysis

H0: Whether cases are nearest neighbors in space is independent of whether they are nearest neighbors in time

Ha: Nearest neighbors in space tend to be nearest neighbors in time

Test statistic: The number of pairs of cases that are k-nearest neighbors in both space and time. K nearest neighbors are the set of cases as near or nearer to a case than the kth nearest neighbor (NN). The cumulative test statistic is: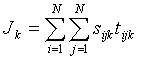

Where sijk is the spatial NN measure (sijk = 1 if case j is a k NN of case i in space and 0 otherwise) and tijk is the time NN measure (tijk = 1 if case j is a k NN of case i in time, and 0 otherwise). The Jk are not independent because case pairs comprising Jk when k is small are included in higher order Jk.

The k-specific test statistic is:

DJk is the number of space-time nearest neighbors added by increasing k by 1. DJk measures space-time interaction above and beyond that observed for the k-1 nearest neighbors. Jk on the other hand, is a cumulative measure of space-time interaction where all nearest neighbor relationships from 1 and k are included. When space-time interaction is present nearby cases will occur at about the same time, (space nearest neighbors tend to be time nearest neighbors), and the test statistic will be large.

Significance of Jk is evaluated using an approximate randomization of the Gamma product. The elements of the matrix of time nearest neighbor measures are shuffled by permuting its rows and columns and Jk is then calculated. This procedure is repeated a fixed number of times, resulting in a distribution of Jk under H0 of no association between space and time nearest neighbor relationships.

Output

Results table includes: